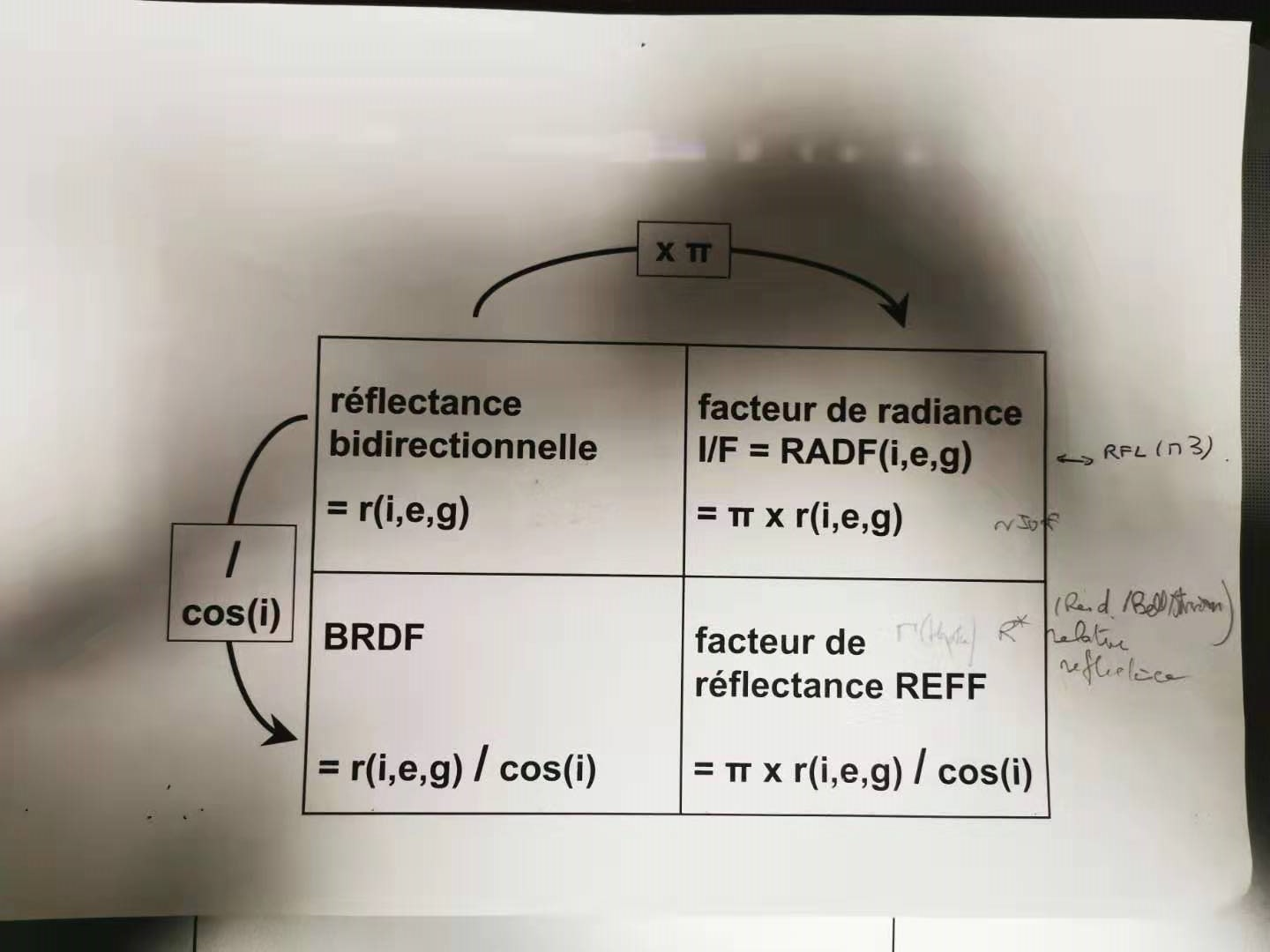
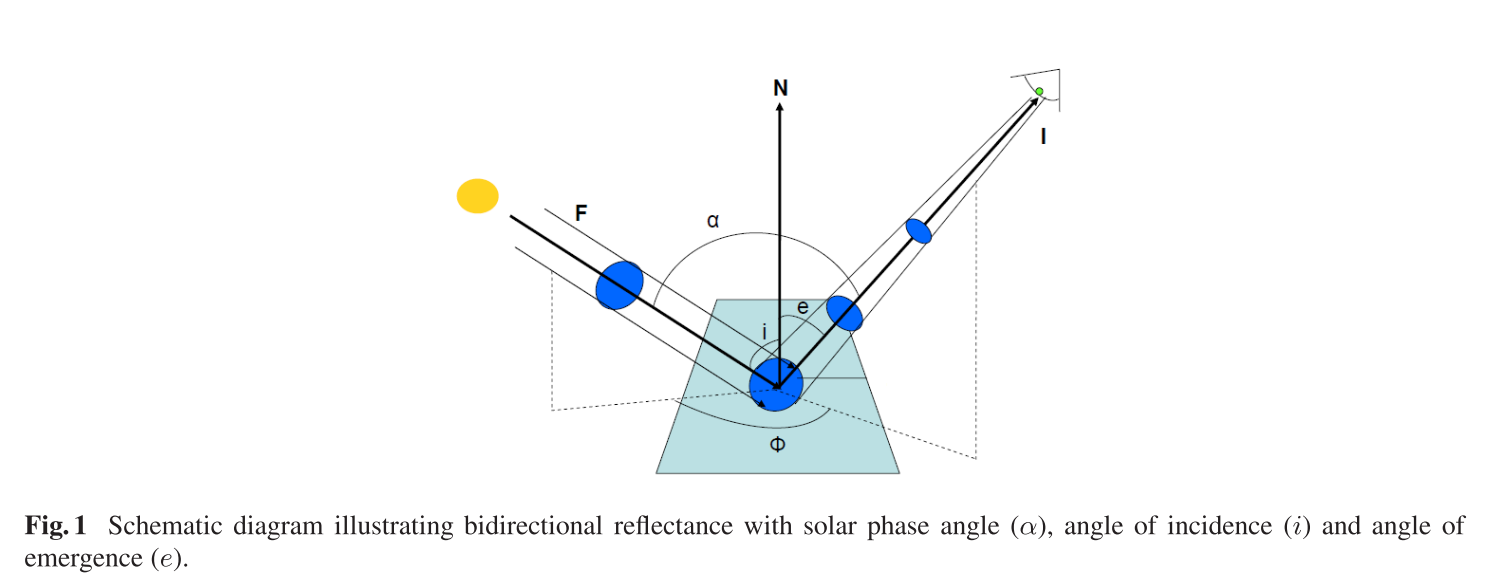
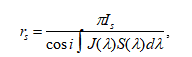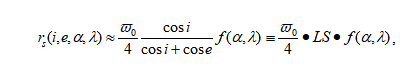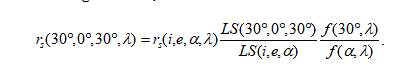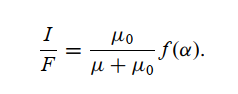Growing

the equation of radiative transfer

发表于 2021-12-17
本文字数： 8.7k 阅读时长 ≈ 8 分钟

Introduction
In most applications of reflectance spectroscopy we are interested in the quantitative amount of light scattered by an infinitely thick layer of large particles.

one way of calculating this is to consider the microscopic processes that occur when a typical particle interacts with the radiation field inside the medium.

Collimated light incident on the medium is partly absorbed and partly scattered by direct encounter with particles in the upper layers.

The light that passes between these particles and the light scattered by them illuminates the given particle where it is partly absorbed and scattered into all directions.

The particle is heated by the light it absorbs and emits thermal radiation.

Some of the radiation scattered or emitted by the particle into an upward-going direction, passes between particles and escapes from the medium.

It is the combined light from all the particles that escapes from the upper surface of the medium that we wish to calculate.

当介质与辐射场共存时，一般有如下几个物理过程:

自发辐射（ spontaneous emission):介质自发地发射光子
吸收（ absorption):部分或全部辐射被介质吸收
受激辐射（ stimulated emission):辐射经过介质时激发介质产生同频率同方向的辐射。
散射（ scattering):入射光子与介质碰撞后改变方向甚至频率

Basic Concepts

Let $\bf{J}= \bf{u}_p J$, where $\bf{u}_p$ is a unit vector pointing in the direction of propagation of $\bf{J}$.

extinction cross section

$\sigma_E = P_E/J$
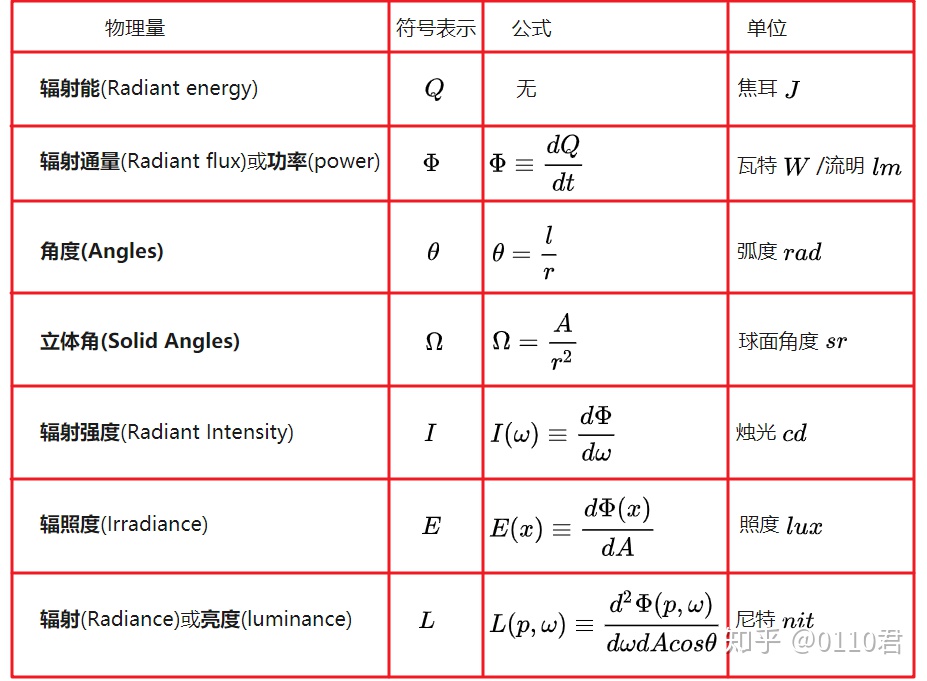
power(功率，单位：W = J/s),irradiance(辐照度，单位：W/m2),所以界面的单位是面积单位，代表概率。
$P_E$ is the total amount of power of $\bf{J}$ that is affected by the particle.

scattering cross section

$\sigma_S = P_S/J$

absorption cross section

$\sigma_A = P_A/J$
An amount $P_S$ of $P_E$ is scattered into all directions, and the reminder $P_A$ is absorbed by the particle.
$P_E = P_S + P_A\\\\ \sigma_E = \sigma_S + \sigma_A$

geometrical cross-sectional area

$\sigma = \pi a^2 \qquad \text{,where a is the particle radius.}$

extinction,scattering and absorption efficiencies

$Q_E = \sigma_E/\sigma,\\\\ Q_S = \sigma_S/\sigma,\\\\ Q_A = \sigma_A/\sigma,\\\\$ $\sigma_E = \sigma_S +\sigma_A.$

截面的单位为面积

系数的单位为1，如大于1，表明比粒子横截面更大范围内的入射光被吸收（散射）

size parameter: the ratio of the circumference of the particle to the wavelength. $X = 2\pi a/\lambda= \pi D/\lambda.$

The ratio of the total amount of power scattered to the total power removed from the wave is the particle single-scattering albedo,$\varpi$.

$\varpi = P_S/P_E = \sigma_S/\sigma_E=Q_S/Q_E$

注：很多文献中，用’A’ 表示。

spat（译作“斯帕特”） function, or the effective single-particle absorption thickness

$W = Q_A/Q_S=\frac{1-\varpi}{\varpi}$

the efficiencies and the single-scattering albedo are functions of wavelength.

Assume that the particles are randomly oriented and positioned.
Let N be the number of particles per unit volume, $\sigma$ be the particle geometric cross-sectional area averaged over all orientations, $Q_E$ be their extinction efficiencies.

Beer’s Law

${dI(s)\over ds = -I(s)N\sigma Q_E}$ $I(S) = I(0)exp(-N\sigma Q_E s)$

extinction coefficient

$E = N\sigma Q_E$

a mixture of different types of particles with $N_j$ particles of type j per unit volume, geometric cross sections averaged over all orieintations $σ_j$, volumes $υ_j$, and extinction, scattering and absorption efficiencies $Q_{Ej}, Q_{Aj}, and Q_{Sj}$, respectively.

Number density(total numper of particles per unit volume)

$N = \sum_j N_j$

average distance $L = N^{-1/3}$

filling factor: the fraction of space within the medium occupied by particles.

$\phi = \sum_j N_j v_j = N v$

$v = \phi/N$ is the avarage volume of a particle.
$1-\phi$ is the porosity.
填充因子是体积比.

volume-average particle cross-sectional area

$\sigma = \left(\sum_j N_j \sigma_j \right) /N$

以上的定义其实是为了理解，真实情况下很难得到一个不规则粒子各个方向的最大截面积的平均值的。

average particle size : the diameter of an equivalent sphere with the average cross-sectional area $\sigma$

$D = \sqrt{4\sigma/\pi}$

volume-average extinction efficiency

$E = \sum_j N_j\sigma_j Q_{Ej} = N\sigma Q_E$

$Q_E = E/{n\sigma}$
volume-average absorption and scattering efficiencies in a similar way.

volume angular scattering coefficient

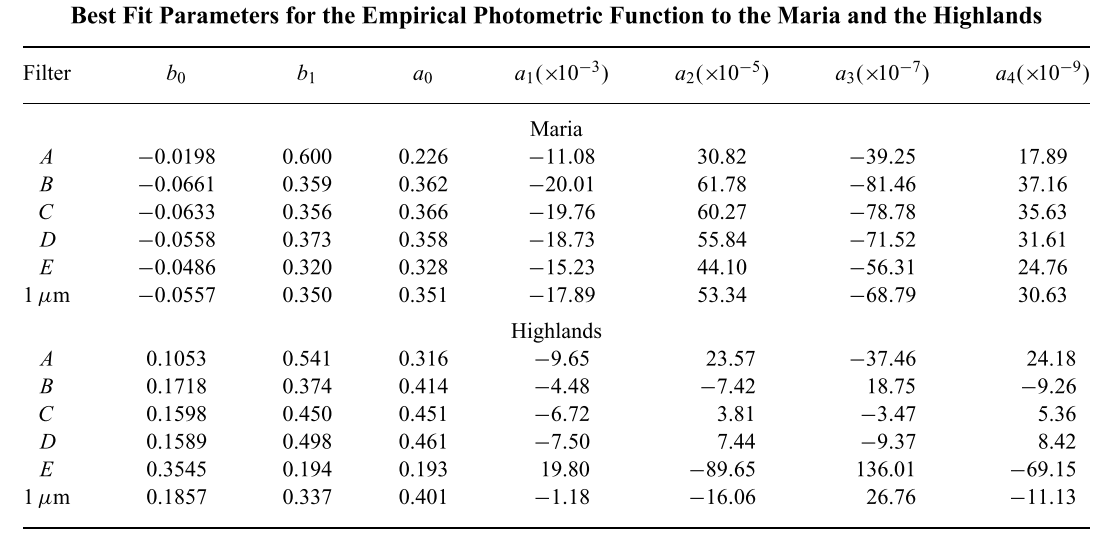
$G(g)=\sum_j N_{j} \sigma_{j} Q_{s j} \Pi_{j}(g)=N \sigma Q_{S} p(g)=S p(g)$

volume-average single-particle phase function

$p(g) = G(g)/S$
normalization condition:
$S=(1 / 2) \int_{0}^{\pi} G(g) \sin g d g, \text { and }(1 / 2) \int_{0}^{\pi} p(g) \sin g d g=1$

volume-average single scattering albedo

$w = S/E$

abeldo factor

$\gamma = \sqrt{1-w}$

volume-average asymmetry factor: the average value of the cosine of the scattering angle θ weighted by the particle phase function

$\xi=<\cos \theta>=-\sum_{j} \frac{1}{2} \int_{0}^{\pi} p(g) \cos g \sin g d g$

extinction mean free path $\Lambda_E$ is the average distance a photon travels through the medium before being extinguished by either absorption or scattering

$\Lambda_{E}=\left(\int_{0}^{\infty} s^{\prime} e^{-E s^{\prime}} d s^{\prime}\right) /\left(\int_{0}^{\infty} e^{-E s^{\prime}} d s^{\prime}\right)=1 / E$

the absorption and scattering mean free paths are in the similar way.

transport coefficient

$S_T = S (1-\xi)$

correspondingly, transport mean free path:$\Lambda_T = 1/(S(1-\xi))$

each of these quantities may depend on both location and direction of the incident radiance.

optical depth

$\tau=\int_{z}^{\infty} E\left(z^{\prime}\right) d z^{\prime}=\int_{s}^{\infty} E\left(s^{\prime}\right) d s^{\prime} / \cos \vartheta$

由于介质的散射和吸收，一束光穿过介质后其强度为$I = I_0 e^{-\int_0^L E(s)ds}= I_)e^{-\tau}$,入射光强随光深成指数减小，$I/I_0 = e^{-\tau}$.从光的粒子属性出发，则$I/I_0 = nh\nu /n_0 h\nu = n/n_0 = e^{-\tau}$。由此可知，光子穿过光深为$\tau$ 的介质逃逸（不被吸收和散射）的概率为$n/n_0= e^{-\tau}$,那么被吸收和散射的概率为$1-e^{-\tau}$. 当介质的光深很小时，光子被吸收或散射的概率为$1-e^{-\tau}\sim \tau$,而当介质的光深为无穷大时，进入介质的光子基本上都被吸收。
$\tau > 1 $的介质称为光学厚的（optical thick）,$\tau < 1 $的介质称为光薄的（optical thin）

transmissivity function

$T\left(s_{1}, s_{2}\right)=\exp \left[-\int_{S_{1}}^{s_{2}} E(s, \Omega) d s\right]$

$I(s_2) = I(s_1) T(s_1,s_2)$

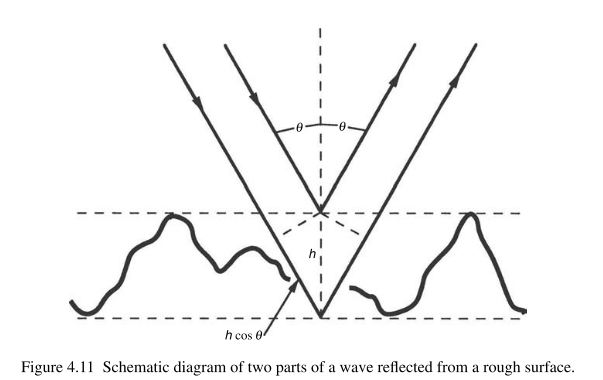
在密堆积粒子中，该式需要作出修正

volume emission coefficient $F(s,\Omega)$ as the power emitted per unit volume by the element at position s into unit solid angle about direction $\Omega$.

$F(s,\Omega) = F_s(s,\Omega) + F_T(s,\Omega)$

single scattering
thermal emission
the general form of the equation of radiative transfer.

$\frac{\partial I(s, \Omega)}{\partial s}=-E(s, \Omega) I(s, \Omega)+\frac{S(s, \Omega)}{4 \pi} \int_{4 \pi} I\left(s, \Omega^{\prime}\right) p\left(s, \Omega^{\prime}, \Omega\right) d \Omega^{\prime}+F(s, \Omega)$

消光项，入射光被散射和吸收后，在入射方向上减少

散射项，从其他方向散射到入射方向的光

发射项，

单次散射项

热发射项，由吸收引起

荧光发射项，一般不考虑

受激辐射项，一般也不考虑，或在吸收系数里加一个负项表示
定义源函数： $F(z, \Omega)=F(z, \Omega) / E(z)$

the parameters of the equqtion of radiative transfer are determined by the properties of the particles making up the medium.

the equqtion of radiative transfer(7.38式)

$\begin{aligned} -\cos \vartheta \frac{\partial I(\tau, \Omega)}{\partial \tau}=&-I(\tau, \Omega)+\frac{w(\tau)}{4 \pi} \int_{4 \pi} I\left(\tau, \Omega^{\prime}\right) p\left(\tau, g^{\prime}\right) d \Omega^{\prime} \\\\ &+J \frac{w(\tau)}{4 \pi} p(\tau, g) e^{-\tau / \cos i}+F_{T}(\tau, \Omega) \end{aligned}$

水平分层介质;
volume single-scattering albedo: $w(z) = S(z)/E(z)$

Radiative transfer in a medium of arbitrary particle separation

Fresnel diffraction in particulate media
Coherent effects in a close-packed medium
The transmissivity of a particulate medium
Radiative transfer in a particulate medium of arbitrary filling factor
Mean free paths in a particulate medium

Methods of solutio of radiactive-transfer problems

求解辐射传输方程(7.5节）

不能精确求解，只有数值解和近似解析解

the Monte Carlo Method
the radiosity method
the doubling method
the Eddington approximation
Integral equation formulation
the multistream method

the multistream method is also called discret ordiantes method.
The sphere of all propagation directions $\Omega$ is broken up into N regions of solid angle $\Delta\Omega_j$ , which need not be equal. The equation of radiative transfer, equation (7.38), is integrated in solid angle over each of the regions $\Delta\Omega_j$ and each resulting equation divided by $\Delta\Omega_j$, giving N equations of the form

$\begin{array}{c} -\frac{1}{\Delta \Omega_{j}} \int_{\Delta \Omega j} \frac{\partial I(\tau, \Omega)}{\partial \tau} \cos \vartheta d \Omega=-\frac{1}{\Delta \Omega_{j}} \frac{\partial}{\partial \tau} \int_{\Delta \Omega j} I(\tau, \Omega) \cos \vartheta d \Omega \\\\ =-\frac{1}{\Delta \Omega_{j}} \int_{\Delta \Omega j} I(\tau, \Omega) d \Omega+\frac{w}{4 \pi} \frac{1}{\Delta \Omega_{j}} \int_{\Delta \Omega_{j}} \int_{4 \pi} p\left(g^{\prime}\right) I\left(\tau, \Omega^{\prime}\right) d \Omega^{\prime} d \Omega \\\\ +J \frac{w}{4 \pi} e^{-\tau / \cos i} \frac{1}{\Delta \Omega_{j}} \int_{\Delta \Omega j} p(g) d \Omega+\frac{1}{\Delta \Omega_{j}} \int_{\Delta \Omega j} F_{T}(\tau) d \Omega \end{array}$

Define the following average quantities for the jth zone:

$\begin{aligned} I_{j}(\tau) &=\frac{1}{\Delta \Omega_{j}} \int_{\Delta \Omega j} I(\tau, \Omega) d \Omega \\\\ \mu_{j} &=\frac{1}{\Delta \Omega_{j}} \int_{\Delta \Omega_{j}} \cos \vartheta d \Omega \\\\ p_{k j} &=\frac{1}{\Delta \Omega_{k}} \frac{1}{\Delta \Omega_{j}} \int_{\Delta \Omega k} \int_{\Delta \Omega j} p\left(g^{\prime}\right) d \Omega^{\prime} d \Omega \\\\ F_{T j}(\tau) &=\frac{1}{\Delta \Omega_{j}} \int_{\Delta \Omega_{j}} F_{T}(\tau, \Omega) d \Omega \end{aligned}$

Note that $p_{kj}$ is the fraction of the radiance traveling in the direction of the center of region k that is scattered into region j.

Then the equation for the intensity in the jth directional region becomes

$\begin{aligned} \mu_{j} d I_{j}(\tau) / d \tau=&-I_{j}(\tau)+(w / 4 \pi) \sum_{k=1}^{\mathcal{N}} \Delta \Omega_{k} p_{k j} I_{k}(\tau) \\\\ &+J \frac{w}{4 \pi} p_{m} e^{-\tau / \cos i}+F_{T j}(\tau) \end{aligned}$

where the region $\Omega_m$ contains the direction to the collimated source, and j takes all integer values between 1 and N.

$p_m = \sum_{k=1}^N p_{mk}$

Thus, the partial integrodifferential equation (7.38) is replaced by a series of N linear, first-order, coupled differential equations that are amenable to well-established numerical solution.

the method of invariance

wavelength dependence

发表于 2021-12-15 更新于 2021-12-16
本文字数： 0 阅读时长 ≈ 1 分钟

Hockey-Stick relation

发表于 2021-12-15 更新于 2023-01-08
本文字数： 2.8k 阅读时长 ≈ 3 分钟

Henyey-Greenstein function

$p(g)=\frac{1+c}{2} \frac{1-b^{2}}{\left(1-2 b \cos (g)+b^{2}\right)^{3 / 2}}+\frac{1-c}{2} \frac{1-b^{2}}{\left(1+2 b \cos (g)+b^{2}\right)^{3 / 2}}$

b (0 ≤ b ≤ 1) is the shape-controlling parameter, and c (−1 ≤ c ≤ 1) is the relative strength of backward and forward lobes.

b is the angular width of the backward (first term) or forward (second term) scattering lobe and c is the magnitude of the lobe.

c>0,后向；c<0 前向

b控制形状：b越大，侧向散射越弱（b=1例外）

Narrow lobes have b values close to 1, wide lobes have values << 1, and isotropically scattering particles have b = 0; 0 <= b < 1.

$p(g)=1$ 表示各向同性；$p(g)\neq 1$ 表示各项异性；$p(g) =0$ 表示完全吸收。

Normalized: ${1\over 4\pi} \int_0^\pi p(g)2\pi \sin g d g = 1$

Asymmetry factor:$<\cos \theta> = {1\over 4\pi} \int_0^\pi \cos\theta p(\theta)2\pi \sin \theta d \theta = -bc$

for a semi-infinite medium, the multiply scattered portion is much less sensitive to the particle phase function than the singly scattered fraction.

The brighter the surface, the more times the average photon is scattered before emerging from the surface, causing directional effects to be averaged out and the multiply scattered intensity distribution to closely approach the isotropic case.

Since the single-scattering term can be evaluated exactly for an arbitrary phase function and the multiply scattered term is relatively insensitive to phase function, a first-order expression for nonisotropic scatterers can be obtained by using the exact expression for the single-scattered term but retaining the isotropic solution for the multiply-scattered term.

多次散射项不像单次散射项那样对相函数明显，通常，表面越亮，多次散射的次数越多，其方向性就被平均掉了，所以一般多次散射项都当做各向同性处理。

hockey stick relation

$c=3.29 \exp \left(-17.4 b^{2}\right)-0.908$

other phase function（经验散射函数见Hapke2012，6.3节）

the Allen approxmation for Fraunhofer diffration
Legendre polynomial
Henyey-Greenstein function
Lambert sphere phase function
Lommel-Seeliger sphere phase function

单参数HG函数

$p(g)=\frac{1-b^{2}}{\left(1+2 b \cos (g)+b^{2}\right)^{3 / 2}}$

$(1/4\pi)\int_{4\pi}p(g)d\Omega = 1$

$\theta = \pi - g$

参数b为余弦不对称因子：$b = <\cos \theta>=-<\cos g>$

b=0时，$p(g)=1$,各向同性

普通多项式（三阶）

$f(g)=p_{1} g^{3}+p_{2} g^{2}+p_{3} g+p_{4}$

普通多项式（四阶）

$f(\alpha)=a_{0}+a_{1} \alpha+a_{2} \alpha^{2}+a_{3} \alpha^{3}+a_{4} \alpha^{4}$

普通多项式（六阶）

$f(\alpha, \lambda)=\mathrm{A}_{0}+\mathrm{A}_{1} \alpha+\mathrm{A}_{2} \mathrm{a}^{2}+\mathrm{A}_{3} \mathrm{\alpha}^{3}+\mathrm{A}_{4} \mathrm{\alpha}^{4}+\mathrm{A}_{5} \mathrm{\alpha}^{5}+\mathrm{A}_{6} \mathrm{\alpha}^{6}$

普通多项式+指数项（指数项模拟背散射效应）

$f(\alpha)=b_{0} e^{-b_{1} \alpha}+a_{0}+a_{1} \alpha+a_{2} \alpha^{2}+a_{3} \alpha^{3}+a_{4} \alpha^{4}$

勒让德多项式

$P(g)=1+b \times \cos (g)+c \times\left(1.5 \times \cos ^{2}(g)-0.5\right)$

$P_1 = \cos \theta; P_2 = {1\over 2}(3\cos^2\theta -1)$

指数形式

$f(\alpha)=e^{\beta \alpha+\gamma \alpha^{2}+\delta \alpha^{3}}$

其他形式：

三阶多项式
一阶勒让德多项式
线性双项HG函数？

Rayleigh scattering

$P(g) = {3\over 4} (1+\cos^2 g)$

Are planetary regolith particles backscattering? (Hapke,1996)

Concepts

Continuous media(连续介质)
particulate media(离散介质): in which the scatters are separated by distance large compared to their size.
regolith: in which the particles are touching.

Roughness

发表于 2021-12-15 更新于 2021-12-17
本文字数： 847 阅读时长 ≈ 1 分钟

path difference（路程差）: $\Delta L = 2 h \cos \theta$

differ in phase（相位差）: $\Delta \phi = 2 \pi \Delta L /\lambda = 4 \pi h \cos \theta /\lambda$.

If $\Delta \phi \ll 2π$, say $\Delta \phi < 2π/10$, then the roughness will have negligible effect on the reflected wave. Thus, one criterion for the surface to be considered smooth would be $h<λsecθ/20$. The so-called Rayleigh criterion is somewhat less stringent（严格） than this and assumes that the effect of roughness will be negligible if $\Delta \phi <π/2$, leading to,

$h < \lambda \sec\theta /8;\quad \text{(瑞利标准)}$

as the criterion for a surface to be considered smooth.

On the other hand, if the two portions of the wave front differ in phase by π or more, then they will certainly interfere with each other, either constructively or destructively, so that the surface will act as a rough scatterer if

$h> \lambda \sec\theta /4$

Note that the roughness criteria depend on θ. A surface may be rough for normal incidence but smooth for glancing incidence（掠入射）.

Opposition Effects

发表于 2021-12-15 更新于 2021-12-17
本文字数： 5.7k 阅读时长 ≈ 5 分钟

1.Opposition Effect

The opposition effect is a sharp surge observed in the reflected brightness of a particulate medium around zero phase angle.

Its name derives from the fac that the phase angle is zero for solar-system objects at astronomical opposition when the Sun, the Earth, and the object are aligned. (译作“冲效应”)

It has many names including the heiligenschein(literally “holy glow”,圣光), hot spot(热点), bright shadow(亮影) and backscatter peak(背散射峰).

On a clear day you can see it as a glow around the shadow of your head when your shadow falls on grass or siol.(It is particularly pronounced in powders with grains a few micrometers in size.

Depending on the marterial the angular width of the peak can range from about $1^\circ$ to more than $20^\circ$.

Compared to some atmosphereless celestial bodies, the Moon reveals a rather wide oppositon surge. For instance, E-type asteroids have the point where the brightness sharply increases in the range $2-3^\circ$, for Kuiper belt objects this angle is even less; whereas, for the Moon it is near $7^\circ$. Usually one assumes a narrow spike to be due to the coherent backscattering, while a wide surge is a result of the shadow-hiding effect. (Shkuratov, Y.G.,2011)

Servral mechanisms have been suggested to explain the opposition effect observed on solar system bodies, including shadow-hiding, coherent backscattering, glories from glass beads, and crystalline corner reflectors. The last two hypotheses can be readily eliminated.

The shadow-hiding opposition effect (SHOE)

The shadow-hiding backscatter surge occurs in any particulate medium in which the grains are larger than the wavelength so that they have shadows. Particles near the surface cast shadows on the deeper grains. The shadows are visiable at large angles, but close to zero phase they are hidden by the objects that cast them.

The opposition effect is particularly pronounced in fine powders with a mean grain size less than about $20\mu m$.

The microstructure formed by fine cohensive powders can be very open, porous, and intricate, consist of lacy towers ande briges(“fairy castle structures”): 分子间静电力和范德华力足以抵抗引力。

The Moon has a strong opposition effect, means that the upper layers of the lunar regolith are fine-grained and have a high porosity.

$B(g) = 1+ B_{S0} B_S(g)$ $B_S(g) \simeq \left(1+{1\over h_S}\tan {g\over 2}\right)^{-1}$

$0\leq B_{S0} \leq 1$.
Considering that light has been scattered only once.

An order-of-magnitude estimate of the expected half-width of the shadow-hiding peak: $HWHM\sim a/\Lambda_E$

The average distance a ray travels in a particlulate medium before encountering a particle and being eithter absorbed or sccattered is the extinction length,$\Lambda_E$, so that this will also be the mean length of a shadow cast by a particle in the medium.

a is the radius of a spherical particle.

The angular width of the SHOE

$HWHM \simeq 2h_S = K E a_E = a_E / \Lambda_E$

K is the porosity factor, $K = -\ln (1- 1.209\phi^{2/3})/1.209\phi^{2/3}$.
E is the Extinctiion coefficient.
$a_E$ is the radius of an equivalent sphere having the cross-sectional area $\sigma_E$. $a_E(z) = \sqrt{\sigma_E(z)/\pi}$, $\sigma_E = <\sigma Q_E>=E(z)/N(z)$

$h_S$ increases as $\phi$ increases and becomes infinite as $\phi \rightarrow 0.752$, so that the peak is infinitely wide. This states that a surface in which the particles are so closely packed that light cannot penetrate between the particles does not have a SHOE.

As $\phi$ decreases, the angular width of the peak narrows.

When the width of the peak becomes much smaller than the angular width of the source or detector as seen form the surface. In this case it is averaged over the combined angular widths of the source and detector and appears as a lower, wider peak.

$h_S = {3\sqrt{3}\over 8}{K\phi \over \ln (a_l/a_s)}$

particle size distribution, power law, $N(a)\propto a^{-\nu}$
$a_l$ and $a_s$ are the largest and smallest particle size.
if $a_l/a_s \simeq 1000$ and $\phi = 0.4$, then $h_S =0.061$, corresponding to a half_width of about $7^\circ$.

The amplitude of the SHOE

the shadow-hiding effect is negligible for the multiply scattered component.

the main effect of multiple scattering is to reduce the height of the peak relative to the total continuum reflectance, which includes both singly and multiply scattered light.

Theoretically, the opposition effect should increase the singly scattered component of the radiance by a factor of exactly 2 at zero phase.

$B_{S0}\simeq S(0)/wp(0)$

$B_{S0}$ is the ratio of the light scattered from near the illuminated portion of the surface of the particle to the total amount of light scattered at zero phase.
$S(0)$ is the fraction of incident light scattered at or close to the illuminated part of the surface oft he particle facing the source,
$wp(0)$ is the total amount of light scattered by the particle at zero phase.

The coherent backscatter opposition effect (CBOE)

An entire different phenomenon can cause a surge in the brightness of a disordered medium at small angles whether the particles are larger or smaller the wavelength.

the phenomenon si known variously as coherent backscatter, time-reversal symmetry, and weak photon localization.

the term weak localization comes from an analogy with the transport of electrons through conducting and semiconducting media. there isa similar phenomenon occurs in the transition region between the conditions where the electrons may be described as waves propagating through the medium and where the electron wave functions become localized on individual atoms. although a photon never becomes permanently confined to an atom it can temporarily follow looping, nearly closed, multiply scattered pathes and, hence, be ‘weakly’ localized.

Part of a wave front incident on a particulate medium encounters a scattering center and is scattered two or more time before exiting the medium at a small phase angle. for very such path another portion of the same wave front will traverse the same path within the medium but in the opposite direction. at large phase angles there is no coherence between the two wavelets and the total intensity is twice the individual intensities. at zero phase angle the two wavelets will be in phase upon emerging from the medium and will combine coherently so as to interfere with each other positively, and the total intensity is quadruple the individual intensities.

$1+B_{C 0} B_{C}(g)$ $B_{C}(g)=\frac{1+\frac{1-\exp \left[-\tan (g / 2) / h_{C}\right]}{\tan (g / 2) / h_{C}}}{2\left[1+\tan (g / 2) / h_{C}\right]^{2}}$

$B_{C0}$ is an empirical quantity that cannot be predicted exactly at the present time, but is related to the albedo.
$h_C = \lambda/4\pi\Lambda$;$\Lambda$ is the transport mean free path in the medium.

Hapke Model

发表于 2021-12-15 更新于 2021-12-16
本文字数： 6.3k 阅读时长 ≈ 6 分钟

Hapke’s photometric model（地大师姐推荐文章(Sato, Robinson et al. 2014)）：也见（Hapke书9.4节（9.47）式）

$I / F=L S\left(i_{e}, e_{e}\right) K \frac{w}{4}\left[p(g)\left(1+B_{S 0} B_{S}(g)\right)+M\left(i_{e}, e_{e}\right)\right]\left[1+B_{C 0} B_{C}(g)\right] S(i, e, \psi)$

注：$I/F$为radiance factor，而reflectance factor(REFF)为${I/F\over \pi}$,这里的I/F就是一种表示方法（RADF），不要分开看。

LS is the Lommel-Seeliger function,$i_e$ and $e_e$ are effective angle of incidence and emission respectively

K is porosity factor,$\phi$,[0,1]

w is single scattering albedo,[0,1]

p(g) is phase function:b,c；The probability that a photon will be scattered in the direction g is given by p(g)。b,[0,1];c,p(g)>0;

$B_{S0}$ is amplitude of Shadow Hiding Opposition Effect (SHOE),Bs,[0,1]

$B_S(g)$ is SHOE function,$h_S$

$M(i_e, e_e)$ is Isotropic Multiple-Scattering Approximation (IMSA)

$B_{C0}$ is amplitude of Coherent Backscatter Opposition Effect (CBOE)，[0,1]

$B_C(g)$ is CBOE function,$h_C$

S(i,e,𝜓) is shadowing function, and 𝜓 is azimuthal angle between the planes of incidence and emergence；The term $\bar{\theta}_p$ is the shadowing function and corrects for macroscopic roughness of the surface and depends on mean slope angle 𝜃.

Henyey-Greenstein double-lobed single particle phase function

$p(g)=\frac{1+c}{2} \frac{1-b^{2}}{\left(1-2 b \cos (g)+b^{2}\right)^{3 / 2}}+\frac{1-c}{2} \frac{1-b^{2}}{\left(1+2 b \cos (g)+b^{2}\right)^{3 / 2}}$

b (0 ≤ b ≤ 1) is the shape-controlling parameter, and c (−1 ≤ c ≤ 1) is the relative strength of backward and forward lobes.
b is the angular width of the backward (first term) or forward (second term) scattering lobe and c is the magnitude of the lobe.
c>0,后向；c<0 前向

b控制形状：b越大，侧向散射越弱（b=1例外）

$p(g)=1$ 表示各向同性；$p(g)\neq 1$ 表示各项异性；$p(g) =0$ 表示完全吸收。

‘hockey-stick” diagram

$c=3.29 \exp \left(-17.4 b^{2}\right)-0.908$
Narrow lobes have b values close to 1, wide lobes have values << 1, and isotropically scattering particles have b = 0; 0 <= b < 1.

Hapke2012,p121

The SHOE function BS(g) is given by

$B_{S}(g)=1 /\left[1+\tan (g / 2) / h_{S}\right]$

$h_S$ is the angular width parameter of SHOE,

The IMSA function $M(i_e, e_e)$ is given by

$M\left(i_{e}, e_{e}\right)=H\left(\frac{\cos \left(i_{e}\right)}{K}, w\right) H\left(\frac{\cos \left(e_{e}\right)}{K}, w\right)-1$

where H(x,w) is Ambartsumian-Chandrasekhar H function, which is approximated by
$H(x, w) \simeq\left\{1-w x\left[r_{0}+\frac{1-2 r_{0} x}{2} \ln \left(\frac{1+x}{x}\right)\right]\right\}^{-1}$
简化版：
$H(x)={1+2x\over 1+2\gamma x}$
$r_0$ is diffusive reflectance, given by
$r_{0}=\frac{1-\sqrt{1-w}}{1+\sqrt{1-w}}$

The CBOE function $B_C(g)$ is given by

$B_{C}(g)=\frac{1+\frac{1-\exp \left[-\tan (g / 2) / h_{C}\right]}{\tan (g / 2) / h_{C}}}{2\left[1+\tan (g / 2) / h_{C}\right]^{2}}$

where $h_C$ is angular width of CBOE

$h_C = \lambda/4\pi\Lambda$;$\Lambda$ is the transport mean free path in the medium.

The porosity factor K is

$K=\frac{-\ln \left(1-1.209 \phi^{2 / 3}\right)}{1.209 \phi^{2 / 3}}$

where 𝜙 is filling factor that is equivalent to 1− porosity. The K monotonically increases with the filling factor 𝜙 (= 1− porosity)

孔隙度因子K不同于孔隙度（porosity）

The $i_e, e_e,$(注：下标e表示effective) and the shadowing function S(i, e,𝜓) are the functions of $\bar{\theta}_p$ (the mean slope angle), the effective value of the photometric roughness.宏观粗糙度。

公式很复杂，待补充

拟合数据得到如上九个参数，这些参数中有些与物性有关

简化的5参数Hapke模型(地大师姐)：SHOE-only.

$I / F={\cos i \over \cos i+\cos e}\frac{w}{4}\left[p(g)\left(1+{B_{S 0} \over 1+\tan(g/2)/h_S}\right)+H(\cos i)H(\cos e)-1\right]$

参数范围：0≤b≤1，-1≤c≤1，0≤w≤1，$0\leq B_{S0} \leq 2$，$0\leq h_S \leq 1$

或者，CBOE-only

在不同的应用场景下，SHOE与CBOE对opposition effects 的贡献不一样，因此，按需选择。得到5参数的hapke模型

$\begin{aligned} \begin{array}{l} \text {IOF} / L S=\frac{w}{4}\left[p(g)+H\left(\mu_{0}, w\right) H(\mu, w)-1\right]\left[1+B_{C 0} B_{C}\left(g, h_{c}\right)\right] S(i, e, \theta) \\ L S=\mu_{0} /\left(\mu_{0}+\mu\right) \end{array} \end{aligned}$

简化hapke模型（林洪磊）:仅3个参数，w,b,c

不考虑冲效应，但考虑多次散射，因此得到3参数的hapke模型，

K= 1，因为月壤最上层的填充率未知

忽略SHOE和COBE，因为冲效应仅仅发生在小相角处，而第十月昼的相角大于50°

$r={\cos i \over \cos i+\cos e}\frac{w}{4\pi}\left[p(g)+H(\cos i)H(\cos e)-1\right]$

若继续不考虑多次散射，则，hapke模型简化为LS模型

Hapke,2012:

Single scattering:the Lommel-Seeliger law（p197)

$r = {\varpi \over 4\pi}{\mu_0 \over \mu_0 +\mu}f(g)$

the bidirectional reflectance of a sparse medium of isotropic scatters(p197)

二流近似

$r = {\varpi \over 4 \pi}{\mu_0\over \mu_0 +\mu}{1+2\mu_0 \over 1+2\gamma\mu_0}{1+2\mu \over 1+2\gamma\mu}$

变分法

$r = {\varpi \over 4 \pi}{\mu_0\over \mu_0 +\mu}H(\mu_0)H(\mu)$

the isotropic multiple-scattering approximation(IMSA)

$I_{SS} = J{\varpi \over 4\pi}{\mu_0 \over \mu_0 +\mu}p(g)$

$I_{MS} = J{\varpi \over 4 \pi}{\mu_0\over \mu_0 +\mu}[H(\mu_0)H(\mu)-1]$

$r = {\varpi \over 4 \pi}{\mu_0\over \mu_0 +\mu}[p(g)+H(\mu_0)H(\mu)-1]$

for a semi-infinite medium, the multiply scattered portion is much less sensitive to the particle phase function than the singly scattered fraction.

相函数有多种形式：

HG函数；

$p(g)=\frac{1+c}{2} \frac{1-b^{2}}{\left(1-2 b \cos (g)+b^{2}\right)^{3 / 2}}+\frac{1-c}{2} \frac{1-b^{2}}{\left(1+2 b \cos (g)+b^{2}\right)^{3 / 2}}$

b = −0.17, c = 0.70。

单参数HG函数

$p(g)=\frac{1-b^{2}}{\left(1+2 b \cos (g)+b^{2}\right)^{3 / 2}}$

$(1/4\pi)\int_{4\pi}p(g)d\Omega = 1$

$\theta = \pi - g$

参数b为余弦不对称因子：$b = <\cos \theta>=-<\cos g>$

b=0时，$p(g)=1$,各向同性

b>0时，

双参数HG函数

$p(g)=\frac{1+c}{2} \frac{1-b^{2}}{\left(1-2 b \cos (g)+b^{2}\right)^{3 / 2}}+\frac{1-c}{2} \frac{1-b^{2}}{\left(1+2 b \cos (g)+b^{2}\right)^{3 / 2}}$

第一项为后向项，第二项为前向项；

三参数HG函数：$b_1,b_2,c$

普通多项式（三阶）

$f(g)=p_{1} g^{3}+p_{2} g^{2}+p_{3} g+p_{4}$

普通多项式（四阶）

$f(\alpha)=a_{0}+a_{1} \alpha+a_{2} \alpha^{2}+a_{3} \alpha^{3}+a_{4} \alpha^{4}$

普通多项式（六阶）

普通多项式+指数项（指数项模拟背散射效应）

$f(\alpha)=b_{0} e^{-b_{1} \alpha}+a_{0}+a_{1} \alpha+a_{2} \alpha^{2}+a_{3} \alpha^{3}+a_{4} \alpha^{4}$

勒让德多项式

$P(g)=1+b \times \cos (g)+c \times\left(1.5 \times \cos ^{2}(g)-0.5\right)$

$P_1 = \cos \theta; P_2 = {1\over 2}(3\cos^2\theta -1)$

指数形式

$f(\alpha)=e^{\beta \alpha+\gamma \alpha^{2}+\delta \alpha^{3}}$

其他形式：

三阶多项式
一阶勒让德多项式
线性双项HG函数？

基于得到的相函数做光度校正：

比值法
解单次反照率：因为多次散射项中包含单次反照率，因此不能直接作比。

以上所有相函数都可用比值法，但HG函数和勒让德多项式来源于Hapke模型，因此还可以基于hapke模型作光度校正。

Hapke函数

发表于 2021-12-15
本文字数： 8.8k 阅读时长 ≈ 8 分钟

photometric correction：将反射率校正到相同的光照几何条件下，一般为入射角30°，出射角0°（NASA实验室所采用的）。比值法

$R_{f-\text {corrected}}=R_{f} \frac{\cos 30^{\circ} /\left(\cos 30^{\circ}+\cos 0^{\circ}\right)}{\cos i^{\prime} /\left(\cos i^{\prime}+\cos e^{\prime}\right)} \frac{f\left(30^{\circ}\right)}{f(g)}$

REFF（Reflectance factor）: solar irradiance calibration method

经验公式：

注：有两种方法获取绝对反射率

定标板

太阳辐照度定标方法

光度校正的公式（注意式子中的约等号）
用Hapke光度模型可以作光度校正，可以反解物性。

月表光度模型研究进展（许学森，遥感技术与应用）

经验模型(hapke8.5节)

几何光学模型

辐射传输模型:Hapke光度模型

计算机数值模拟方法：蒙托卡罗数值模拟方法

Hapke’s photometric model（地大师姐推荐文章(Sato, Robinson et al. 2014)）：也见（Hapke书9.4节（9.47）式）

$I / F=L S\left(i_{e}, e_{e}\right) K \frac{w}{4}\left[p(g)\left(1+B_{S 0} B_{S}(g)\right)+M\left(i_{e}, e_{e}\right)\right]\left[1+B_{C 0} B_{C}(g)\right] S(i, e, \psi)$

注：$I/F$为radiance factor，而reflectance factor(REFF)为${I/F\over \pi}$,这里的I/F就是一种表示方法（RADF），不要分开看。

LS is the Lommel-Seeliger function,$i_e$ and $e_e$ are effective angle of incidence and emission respectively

K is porosity factor,$\phi$,[0,1]

w is single scattering albedo,[0,1]

p(g) is phase function:b,c；The probability that a photon will be scattered in the direction g is given by p(g)。b,[0,1];c,p(g)>0;

$B_{S0}$ is amplitude of Shadow Hiding Opposition Effect (SHOE),Bs,[0,1]

$B_S(g)$ is SHOE function,$h_S$

$M(i_e, e_e)$ is Isotropic Multiple-Scattering Approximation (IMSA)

$B_{C0}$ is amplitude of Coherent Backscatter Opposition Effect (CBOE)，[0,1]

$B_C(g)$ is CBOE function,$h_C$

S(i,e,𝜓) is shadowing function, and 𝜓 is azimuthal angle between the planes of incidence and emergence；The term $\bar{\theta}_p$ is the shadowing function and corrects for macroscopic roughness of the surface and depends on mean slope angle 𝜃.

Henyey-Greenstein double-lobed single particle phase function

$p(g)=\frac{1+c}{2} \frac{1-b^{2}}{\left(1-2 b \cos (g)+b^{2}\right)^{3 / 2}}+\frac{1-c}{2} \frac{1-b^{2}}{\left(1+2 b \cos (g)+b^{2}\right)^{3 / 2}}$

b (0 ≤ b ≤ 1) is the shape-controlling parameter, and c (−1 ≤ c ≤ 1) is the relative strength of backward and forward lobes.
b is the angular width of the backward (first term) or forward (second term) scattering lobe and c is the magnitude of the lobe.
c>0,后向；c<0 前向

b控制形状：b越大，侧向散射越弱（b=1例外）

$p(g)=1$ 表示各向同性；$p(g)\neq 1$ 表示各项异性；$p(g) =0$ 表示完全吸收。

‘hockey-stick” diagram

$c=3.29 \exp \left(-17.4 b^{2}\right)-0.908$
Narrow lobes have b values close to 1, wide lobes have values << 1, and isotropically scattering particles have b = 0; 0 <= b < 1.

Hapke2012,p121

The SHOE function BS(g) is given by

$B_{S}(g)=1 /\left[1+\tan (g / 2) / h_{S}\right]$

$h_S$ is the angular width parameter of SHOE,

The IMSA function $M(i_e, e_e)$ is given by

$M\left(i_{e}, e_{e}\right)=H\left(\frac{\cos \left(i_{e}\right)}{K}, w\right) H\left(\frac{\cos \left(e_{e}\right)}{K}, w\right)-1$

where H(x,w) is Ambartsumian-Chandrasekhar H function, which is approximated by
$H(x, w) \simeq\left\{1-w x\left[r_{0}+\frac{1-2 r_{0} x}{2} \ln \left(\frac{1+x}{x}\right)\right]\right\}^{-1}$
简化版：
$H(x)={1+2x\over 1+2\gamma x}$
$r_0$ is diffusive reflectance, given by
$r_{0}=\frac{1-\sqrt{1-w}}{1+\sqrt{1-w}}$

The CBOE function $B_C(g)$ is given by

$B_{C}(g)=\frac{1+\frac{1-\exp \left[-\tan (g / 2) / h_{C}\right]}{\tan (g / 2) / h_{C}}}{2\left[1+\tan (g / 2) / h_{C}\right]^{2}}$

where $h_C$ is angular width of CBOE

$h_C = \lambda/4\pi\Lambda$;$\Lambda$ is the transport mean free path in the medium.

The porosity factor K is

$K=\frac{-\ln \left(1-1.209 \phi^{2 / 3}\right)}{1.209 \phi^{2 / 3}}$

where 𝜙 is filling factor that is equivalent to 1− porosity. The K monotonically increases with the filling factor 𝜙 (= 1− porosity)

孔隙度因子K不同于孔隙度（porosity）

The $i_e, e_e,$(注：下标e表示effective) and the shadowing function S(i, e,𝜓) are the functions of $\bar{\theta}_p$ (the mean slope angle), the effective value of the photometric roughness.宏观粗糙度。

公式很复杂，待补充

拟合数据得到如上九个参数，这些参数中有些与物性有关

简化的5参数Hapke模型(地大师姐)：SHOE-only.

$I / F={\cos i \over \cos i+\cos e}\frac{w}{4}\left[p(g)\left(1+{B_{S 0} \over 1+\tan(g/2)/h_S}\right)+H(\cos i)H(\cos e)-1\right]$

参数范围：0≤b≤1，-1≤c≤1，0≤w≤1，$0\leq B_{S0} \leq 2$，$0\leq h_S \leq 1$

或者，CBOE-only

在不同的应用场景下，SHOE与CBOE对opposition effects 的贡献不一样，因此，按需选择。得到5参数的hapke模型

简化hapke模型（林洪磊）:仅3个参数，w,b,c

不考虑冲效应，但考虑多次散射，因此得到3参数的hapke模型，

K= 1，因为月壤最上层的填充率未知

忽略SHOE和COBE，因为冲效应仅仅发生在小相角处，而第十月昼的相角大于50°

$r={\cos i \over \cos i+\cos e}\frac{w}{4\pi}\left[p(g)+H(\cos i)H(\cos e)-1\right]$

若继续不考虑多次散射，则，hapke模型简化为LS模型

Hapke,2012:

Single scattering:the Lommel-Seeliger law（p197)

$r = {\varpi \over 4\pi}{\mu_0 \over \mu_0 +\mu}f(g)$

the bidirectional reflectance of a sparse medium of isotropic scatters(p197)

二流近似

$r = {\varpi \over 4 \pi}{\mu_0\over \mu_0 +\mu}{1+2\mu_0 \over 1+2\gamma\mu_0}{1+2\mu \over 1+2\gamma\mu}$

变分法

$r = {\varpi \over 4 \pi}{\mu_0\over \mu_0 +\mu}H(\mu_0)H(\mu)$

the isotropic multiple-scattering approximation(IMSA)

$I_{SS} = J{\varpi \over 4\pi}{\mu_0 \over \mu_0 +\mu}p(g)$

$I_{MS} = J{\varpi \over 4 \pi}{\mu_0\over \mu_0 +\mu}[H(\mu_0)H(\mu)-1]$

$r = {\varpi \over 4 \pi}{\mu_0\over \mu_0 +\mu}[p(g)+H(\mu_0)H(\mu)-1]$

for a semi-infinite medium, the multiply scattered portion is much less sensitive to the particle phase function than the singly scattered fraction.

一些光度校正的实操论文

问题：参数拟合的数学实现以及遇见的一些细节问题

python拟合函数curve_fit

参数初始值问题：若不给初值，也不给边界，则初值默认为1；若不给初值，但给定边界，则初值为边界中点。

python 其他函数

lunar opposition effect（Hapke第九章）

shadow hiding（占主要）：shadow-hiding mechanism in which particles hide their own shadows at opposition but the shadows quickly become visible as one moves away from opposition（clementine Hillier 1999）
相干反向散射coherent backscatter（2°左右的窄峰）： photons following identical but reversed paths can interfere constructively in the backscattering direction, leading to up to a factor of two increase in brightness.
具有波长依赖性
the angular width of the coherent backscatter peak should be proportional to wavelength, it is inversely proportional to the mean optical path length of a photon (which will be smaller in lower albedo surfaces)
相干反向散射对更亮的高地地形更重要

ground truth: Apollo site

photometric model 可反演月壤的物理性质

compaction state
particle albedo
particle size
size distribution
surface macroscopic roughness
grain transparency
porosity
光度模型可以反演上述参数，然后用反演的参数与Apollo的“真值”对比，可以检验光度模型理论
相对定标：矿物学研究
绝对定标：光度研究、

从反射率光谱获取矿物成分：

查找表（lunar spectral mineral lookup table，LUT）
MGM(修正高斯模型)
其他？
实操过程：

光度校正公式（前经验）：

Scattering Law Analysis Based on Hapke and Lommel-Seeliger Models for Asteroidal Taxonomy
Hapke-5parameters

$\begin{aligned} RADF(i, e, \alpha)&=\frac{\omega}{4} \frac{\mu_{0}}{\mu_{0}+\mu} \\\\ & \times\left\{[1+B(\alpha)] p(\alpha)+H\left(\mu_{0}\right) H(\mu)-1\right\} \\\\ & \times S(i, e, \alpha, \bar{\theta}) \\\\ B(\alpha)&=\frac{B_{\mathrm{so}}}{1+\frac{1}{h_{\mathrm{s}}} \tan \frac{\alpha}{2}} \\\\ p(\alpha)&=\frac{1-g^{2}}{\left(1+2 g \cos \alpha+g^{2}\right)^{\frac{3}{2}}} \\\\ H(x)&=\frac{1+2 x}{1+2 \sqrt{1-\omega} x} \end{aligned}$

-LS模型

$\begin{aligned} r(i, e, \alpha)&=A_{\mathrm{ls}} \frac{\mu_{0}}{\mu_{0}+\mu} f(\alpha)\\\\ A_{ls} &={\omega \over 4\pi}\\\\ f(\alpha)&=e^{\beta \alpha+\gamma \alpha^{2}+\delta \alpha^{3}}\\\\ RADF(i,e,\alpha)&= \pi r(i,e,g) \end{aligned}$

光度校正的关键在于获取相函数及其参数。

获取相函数的两种模型：

Hapke模型
LS模型

相函数有多种形式：

HG函数；

$p(g)=\frac{1+c}{2} \frac{1-b^{2}}{\left(1-2 b \cos (g)+b^{2}\right)^{3 / 2}}+\frac{1-c}{2} \frac{1-b^{2}}{\left(1+2 b \cos (g)+b^{2}\right)^{3 / 2}}$

b = −0.17, c = 0.70。

单参数HG函数

$p(g)=\frac{1-b^{2}}{\left(1+2 b \cos (g)+b^{2}\right)^{3 / 2}}$

$(1/4\pi)\int_{4\pi}p(g)d\Omega = 1$

$\theta = \pi - g$

参数b为余弦不对称因子：$b = <\cos \theta>=-<\cos g>$

b=0时，$p(g)=1$,各向同性

b>0时，

双参数HG函数

$p(g)=\frac{1+c}{2} \frac{1-b^{2}}{\left(1-2 b \cos (g)+b^{2}\right)^{3 / 2}}+\frac{1-c}{2} \frac{1-b^{2}}{\left(1+2 b \cos (g)+b^{2}\right)^{3 / 2}}$

第一项为后向项，第二项为前向项；

三参数HG函数：$b_1,b_2,c$

普通多项式（三阶）

$f(g)=p_{1} g^{3}+p_{2} g^{2}+p_{3} g+p_{4}$

普通多项式（四阶）

$f(\alpha)=a_{0}+a_{1} \alpha+a_{2} \alpha^{2}+a_{3} \alpha^{3}+a_{4} \alpha^{4}$

普通多项式（六阶）

普通多项式+指数项（指数项模拟背散射效应）

$f(\alpha)=b_{0} e^{-b_{1} \alpha}+a_{0}+a_{1} \alpha+a_{2} \alpha^{2}+a_{3} \alpha^{3}+a_{4} \alpha^{4}$

勒让德多项式

$P(g)=1+b \times \cos (g)+c \times\left(1.5 \times \cos ^{2}(g)-0.5\right)$

$P_1 = \cos \theta; P_2 = {1\over 2}(3\cos^2\theta -1)$

指数形式

$f(\alpha)=e^{\beta \alpha+\gamma \alpha^{2}+\delta \alpha^{3}}$

其他形式：

三阶多项式
一阶勒让德多项式
线性双项HG函数？

基于得到的相函数做光度校正：

比值法
解单次反照率：因为多次散射项中包含单次反照率，因此不能直接作比。

以上所有相函数都可用比值法，但HG函数和勒让德多项式来源于Hapke模型，因此还可以基于hapke模型作光度校正

光度校正历史

Clementine （Hiller et al,1999）

M3
SELENE
CE-1
CE-3
CE-4

几组HG函数参数：

b = −0.17， c = 0.70。

(Yang,Yazhou,2020;Lin,Honglei,2020)
CE-4,第十月昼

b = −0.4, c = 0.25。

(lucey,1998)
假定参数

b=0.3,c =0.08

(Jin,Weidong,2015)
CE-3,全景相机，460nm,9参数Hapke模型
若使用5参数Hapke模型，b=0.32,c=-0.17

待办

[ ] 光度模型溯源文章
[ ] 光端校正文章内容
[ ] hapke模型

hapke模型的拟合

前人怎么拟合的

网格搜索；遗传算法；查找表，等！
求解全局最小的算法及其原理！

误差传递公式

发表于 2021-12-10 更新于 2021-12-13
本文字数： 223 阅读时长 ≈ 1 分钟

总的公式：

$z = f(x,y)$ $\sigma_z^2 = \left({\partial f \over \partial x}\right)^2 \sigma_x^2 + \left({\partial f \over \partial y}\right)^2 \sigma_y^2$

示例：

$\bar{x} = {1\over n}\sum_{i=1}^{n} x_i$ $\sigma_{\bar{x}} = {1\over n}\sqrt{\sum_{i=1}^{n} \sigma_{x_i}^2}$

关于个人网站的学习资源总结

发表于 2021-12-08 更新于 2022-07-05
本文字数： 413 阅读时长 ≈ 1 分钟

1. 博客：github+hexo

https://hexo.io/zh-cn/docs/commands.html

https://yuumiy.github.io/posts/2789.html

https://www.jianshu.com/p/9b9c241146bc

Hexo博客写文章及基本操作 - Unity晚阳的文章 - 知乎 https://zhuanlan.zhihu.com/p/156915260

2. 个人主页： GitHub + jekyll

3. 学术主页： github+hugo+netlify

【Hugo+Netlify】制作英文学术个人简介网站（一）：基础版 - Magical-E的文章 - 知乎 https://zhuanlan.zhihu.com/p/110137145

https://www.bilibili.com/video/BV1iA411v7Gi/

https://ianying.vercel.app/laymanit/

Chapter 10

发表于 2021-12-06
本文字数： 6.1k 阅读时长 ≈ 6 分钟

补充知识：
辐射度量

辐射能量（Radiant energy,Q）：电磁辐射的能量，J(焦耳)

使被照物体温度升高；改变物体的内部状态；是带电物体受力而运动

辐射通量(Radiant flux):单位时间内通过某一面积的辐射能量，W(瓦特),也称为功率（power）

$\Phi= dQ/dt$

辐射通量密度:单位面积上的辐射通量,$W/m^2$

$d\Phi/dS$

辐射照度（Irradiance,E);单位面积被辐射物体所接收的辐射通量

$E = d\Phi/dS$

辐照度衰减：

$E^\prime = {\Phi \over 4\pi r^2}$

兰伯特余弦定律：表面辐照度与光方向和表面法线夹角的余弦值成正比(也就是说只要在表面法线方向的的辐射度分量)。

辐射出射度（Radiant exitance）:单位面积上辐射源辐射出的辐射通量

$M =d\Phi/dS$

辐射强度（Radiant Intensity）:点辐射源在单位立体角内的辐射通量,$W/Sr$

$I = d\Phi/d\Omega$

对各向同性点源，$I = {\Phi \over 4\pi}$; $W/Sr$

辐射（Radiance,也称亮度，luminance,L）:辐射源在单位投影面积上、单位立体角内的辐射通量，

$L(\theta) = \frac{d^2\Phi}{d\Omega dA \cos\theta}=\frac{dM}{d\Omega \cos \theta}$
最重要概念

Radiant Flux,辐射通量，光通量，辐射功率；在单位时间穿过截面的光能；单位是W，瓦特

(Radiant) Intensity, 辐射强度，发光强度；每单位立体角的辐射通量；单位，瓦特每球面度。

Radiance, 光亮度，辐亮度，辐射率；每单位立体角每单位投影面积的辐射通量；瓦特每球面度每平方米。

Irradiance, 辐照度，辉度，辐射照度；单位时间内到达单位面积的辐射通量，也就是辐射通量对于面积的密度；瓦特每平方米。

详情可参考：辐射度量学 - 知乎

10.2 some commonly encountered bidirectional reflectance quantities

the bidirectional reflectance $r(i,e,g)$

$r(i,e,g)= K\frac{\varpi}{4\pi}\frac{\mu_0}{\mu_0+\mu}\left[P(g)+H(\mu_0/K)H(\mu/K)-1\right]$

the bidirectional reflectance is the ratio of the radiance scattered from the surface of a medium into a given direction to the collimated power incident per area perpendicular to the direction of the incidence.

K is the porosity coefficients.

孔隙率：土壤中孔隙体积与总体积的比值。

$r(i,e,g)=\dfrac{emit_radiance}{incident_irradiance}=\dfrac{I_e}{J}.$

X.-J. Huang et al.: Analysis Based on the Hapke Model and LS Model

the bidirectional-reflectance distribution function (BDRF)

$\begin{aligned} BDRF(i,e,g)=&\frac{I}{J\mu_0}=\frac{r(i,e,g)}{\mu_0}\\ =&K\frac{\varpi}{4\pi}\frac{1}{\mu_0+\mu}\left[P(g)+H(\mu_0/K)H(\mu/K)-1\right] \end{aligned}$

the bidirectional-reflectance distribution function (BDRF) is the ratio of the radiance scattered from the surface of a medium into a given direction to the collimated power incident on a unit area of the surface.

the reflectance factor (REFF), is also called the _reflectance coefficient (or, apparent reflectance)._

$\small REFF(i,e,g)= \pi r(i,e,g)/\mu_0=K\frac{\varpi}{4}\frac{1}{\mu_0+\mu}\left[P(g)+H(\mu_0/K)H(\mu/K)-1\right]$

the reflectance factor is the ratio of the reflectance of the surface to that of a perfectly diffuse surface under the same conditions of illumination and measurement.
the bidirectional reflectance of a perfect Lambert surface is

$r_L =\mu_0/\pi$

for details(8.5.1 Lambert’s law)

reflectance factor: 即测量到的反射率$I/J$与相同光照条件下的朗伯体的反射率$\cos i/\pi$之比。

the radiance factor (RADF), is also denoted by I/F.

$\begin{aligned} RADF(i,e,g)=&\frac{I}{F}(i,e,g)=\pi r(i,e,g) \\=&K\frac{\varpi}{4}\frac{\mu_0}{\mu_0+\mu}\left[P(g)+H(\mu_0/K)H(\mu/K)-1\right] \end{aligned}$

the radiance factor is the ratio of the bidirectional reflectance of a surface to that of a perfectly diffuse surface illuminated at
$i = 0,r_L=1/\pi$
, rather than at the same angle of illumination as the sample.

$F=J/\pi$, Chandrasekhar (1960).

Shkuratov,2011称：在老文章里，也称apparent albedo.（不够准确，权当历史原因造成）。

the relative reflectance ,

$\begin{aligned} \Gamma(i,e,g)=&\frac{r(Sample)}{r(standard\_surface)}\\ = &\frac{K_{Sa}}{K_{St}}\varpi\frac{P(g)+H(\mu_0/K_{Sa},\varpi)H(\mu/K_{Sa},\varpi)-1}{H(\mu_0/K_{St},\varpi=1)H(\mu/K_{St},\varpi=1)} \end{aligned}$

the relative reflectance of a particulate sample is the reflectance relative to that of standard surface consisting of an infinitely thick particulate medium of nonabsorbing, isotropic scatterers, with negligible opposition effect, and illuminated and viewed at the same geometry as the sample.

if
$K_{Sa}=K_{St}\approx 1$
, and the H functions
$H(x)\simeq \frac{1+2x}{1+2\gamma x}$
, the relative bidirectional reflectance of a sample of isotropic scatterers measured outside of the opposition peak is given by
$\Gamma(i,e,g\gg h)=\frac{\varpi}{(1+2\gamma\mu_0)(1+2\gamma\mu)}$

the reduced reflectance $r_r(i,e,g)$

$r_r(i,e,g) =\frac{I/F}{\mu_0/(\mu_0 +\mu)}$

the reduced reflectance is defined as the radiance factor divided by the Lommel-Seeliger factor.

计算过程中通常还需要校正太阳距离：

加州理工大学，喷气动力实验室，JPL：https://ssd.jpl.nasa.gov/horizons.cgi （地平线系统！）

补充知识

反射率波谱

方向-方向反射率波谱（晴天，野外便携式地物光谱仪）

半球 -方向反射率波谱（阴天）

方向-半球反射率波谱（积分球，波谱测定器）;directional-hemispherical reflectance.

半球- 半球反射率波谱（等效于反照率光谱）

朗伯体：
朗伯体：是指当入射能量在所有方向均匀反射，即入射能量以入射点为中心，在整个半球空间内向四周各向同性的反射能量的现象，称为漫反射，也称各向同性反射，一个完全的漫射体称为朗伯体。理想的漫反射应遵循这个规律。例如积雪和白墙。
余弦发光体：若一扩展光源的发光强度为dI∝cosθ，即其亮度B与方向无关。这类发射体称为余弦发光体，或朗伯（J.H.Lambert）发光体，上述按cosθ规律发射光通量的规律，成为朗伯余弦定律。式中dI为扩展光表面的每块面元dS沿某方向r的发光强度，θ为r与法线n的夹角。
从远处看，发光球体像是一个发光圆盘，这就是余弦发光体，太阳就是余弦发光体。
物体表面对电磁波的反射有三种形式：

镜面反射：反射能量集中在一个方向，反射角=入射角。

漫反射：整个表面都均匀地向各向反射入射光。

方向反射：介于漫反射和镜面反射之间，各向都有反射，但各向反射强度不均一。实际上多数自然表面对辐射的波长而言都是粗糙表面。当目标物的表面足够粗糙，以致于它对太阳短波辐射的反射辐射亮度在以目标物的中心的2π空间中呈常数，即反射辐射亮度不随观测角度而变，我们称该物体为漫反射体，亦称朗伯体。漫反射又称朗伯(Lambert)反射，也称各向同性反射。

对反射率的一些思考（从量纲量级角度）：

牢记双向反射率的定义：

$r= I/J \quad [Sr^{-1}]$

假如没有吸收，且反射在$2\pi$空间内各向同性(朗伯体)，则某一表面

入射能量：$P_{in} = J\mu_0 = J (i =0)$

出射能量：$P_{out} = \int I cos e d\Omega = \int J r \cos e \sin ede d\varphi = J \pi[Sr] r [Sr^{-1}]$

能量守恒：

$P_{in} = P_{out} \Rightarrow r = {1\over \pi}$
各种反射率的范围：

BDR = r: 理想朗伯体为$1/\pi$；$[0,1/\pi]$
BDRF = r/cos(i): 范围待分析，本人研究过程中不常用！
RADF = $\pi r$: $[0,1]$
REFF = ${r\over cos i /\pi}$: $[0,1]$ (理想朗伯体的双向反射率最大！)

对理想朗伯体而言，半球反射率与反射率因子在数值上相等：

理想朗伯体的双向反射率：$r = cos i /\pi$

设朗伯体表面积为S,入射辐照度为J,入射角为i,出射角为$\theta$,方位角为$\varphi$,则:
按定义，$r = I/J$
入射通量为：$\Phi_i = J S cos i$
出射通量为：

$\Phi_o = \int I S_\perp d\Omega = \int (rJ)(S cos\theta)d\Omega = rJS \int_0^{2\pi}\int_0^{\pi/2} cos\theta sin\theta d\theta d\varphi = rJS\pi$

按定义，半球反射率，$r_{dh} = {\Phi_o \over \Phi_i}= {rJS\pi \over JS cos i}= {\pi r \over cos i}$
于是，可推导出，$r = r_{dh} cos i/\pi$
进而，按定义，$REFF = {r \over cos i/\pi}= r_{dh}$

考虑入射角为0的朗伯平面（perfectly diffuse surface）：

$r = 1/\pi$

从反照率

$A_L= {P_{out} \over J\mu_0} =1 \Rightarrow P_{out} = J = P_{in}; (\mu_0 =1)$
满足能量守恒

从双向反射率：

$r = I/J = 1/\pi \Rightarrow I = Jr = J/\pi \Rightarrow \\P_{out} = \int_{上半球} I\mu d\Omega = J/\pi \int_{e=0}^{\pi/2} \cos e \sin e de \int_{\psi =0}^{2\pi} = J = P_{in}$
满足能量守恒

但

$\int_{上半球} r d\Omega = 2 \neq 1$

$RADF = \pi r =1$ ;因为完全反射，所以在各个方向上，$RADF=1$。

基尔霍夫定律：发射率= 吸收率=1-反射率（在各个方向上都满足），

For an arbitrary body emitting and absorbing thermal radiation in thermodynamic equilibrium, the emissivity is equal to the absorptivity.

a good absorber is a good emitter, and a poor absorber is a poor emitter,a good reflector must be a poor absorber.

In a blackbody enclosure that contains electromagnetic radiation with a certain amount of energy at thermodynamic equilibrium, this “photon gas” will have a Planck distribution of energies.

black body radiation is equal in every direction (isotropic), the emissivity and the absorptivity, if they happen to be dependent on direction, must again be equal for any given direction.

此处的反射率不是双向反射率。

Kirchhoff ’s law applies to directional–hemispherical reflectance。(Bandfield,2018)
-

Henyey-Greenstein function

hockey stick relation

other phase function（经验散射函数见Hapke2012，6.3节）

Rayleigh scattering

Are planetary regolith particles backscattering? (Hapke,1996)

Concepts

1. 博客：github+hexo

2. 个人主页： GitHub + jekyll

3. 学术主页： github+hugo+netlify

10 A miscellany of bidirectional reflectances and related quantities

10.2 some commonly encountered bidirectional reflectance quantities