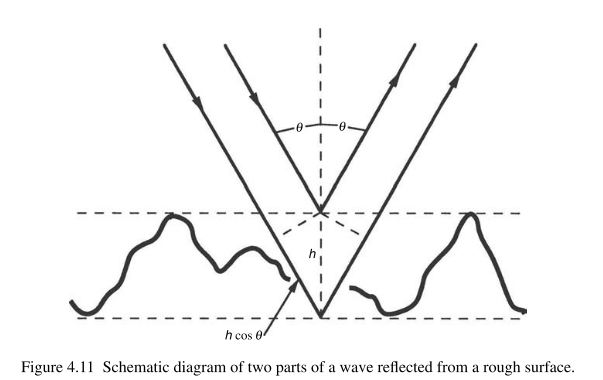
path difference(路程差): $\Delta L = 2 h \cos \theta$
differ in phase(相位差): $\Delta \phi = 2 \pi \Delta L /\lambda = 4 \pi h \cos \theta /\lambda$.
If $\Delta \phi \ll 2π$, say $\Delta \phi < 2π/10$, then the roughness will have negligible effect on the reflected wave. Thus, one criterion for the surface to be considered smooth would be $h<λsecθ/20$. The so-called Rayleigh criterion is somewhat less stringent(严格) than this and assumes that the effect of roughness will be negligible if $\Delta \phi <π/2$, leading to,
as the criterion for a surface to be considered smooth.
On the other hand, if the two portions of the wave front differ in phase by π or more, then they will certainly interfere with each other, either constructively or destructively, so that the surface will act as a rough scatterer if
Note that the roughness criteria depend on θ. A surface may be rough for normal incidence but smooth for glancing incidence(掠入射).