Chapter 10

10 A miscellany of bidirectional reflectances and related quantities

补充知识：
辐射度量

1. 辐射能量（Radiant energy,Q）：电磁辐射的能量，J(焦耳)

使被照物体温度升高；改变物体的内部状态；是带电物体受力而运动

1. 辐射通量(Radiant flux):单位时间内通过某一面积的辐射能量，W(瓦特),也称为功率（power）

$$\Phi= dQ/dt$$

1. 辐射通量密度:单位面积上的辐射通量,$W/m^2$

$$d\Phi/dS$$

1. 辐射照度（Irradiance,E);单位面积被辐射物体所接收的辐射通量

$$E = d\Phi/dS$$

• 辐照度衰减：

$$E^\prime = {\Phi \over 4\pi r^2}$$

• 兰伯特余弦定律：表面辐照度与光方向和表面法线夹角的余弦值成正比(也就是说只要在表面法线方向的的辐射度分量)。
• 辐射出射度（Radiant exitance）:单位面积上辐射源辐射出的辐射通量

$$M =d\Phi/dS$$

1. 辐射强度（Radiant Intensity）:点辐射源在单位立体角内的辐射通量,$W/Sr$

$$I = d\Phi/d\Omega$$

对各向同性点源，$I = {\Phi \over 4\pi}$; $W/Sr$

1. 辐射（Radiance,也称亮度，luminance,L）:辐射源在单位投影面积上、单位立体角内的辐射通量，

$$L(\theta) = \frac{d^2\Phi}{d\Omega dA \cos\theta}=\frac{dM}{d\Omega \cos \theta}$$

最重要概念

• Radiant Flux,辐射通量，光通量，辐射功率；在单位时间穿过截面的光能；单位是W，瓦特
• (Radiant) Intensity, 辐射强度，发光强度；每单位立体角的辐射通量；单位 ，瓦特每球面度。
• Radiance, 光亮度，辐亮度，辐射率；每单位立体角每单位投影面积的辐射通量；瓦特每球面度每平方米。
• Irradiance, 辐照度，辉度，辐射照度；单位时间内到达单位面积的辐射通量，也就是辐射通量对于面积的密度；瓦特每平方米。

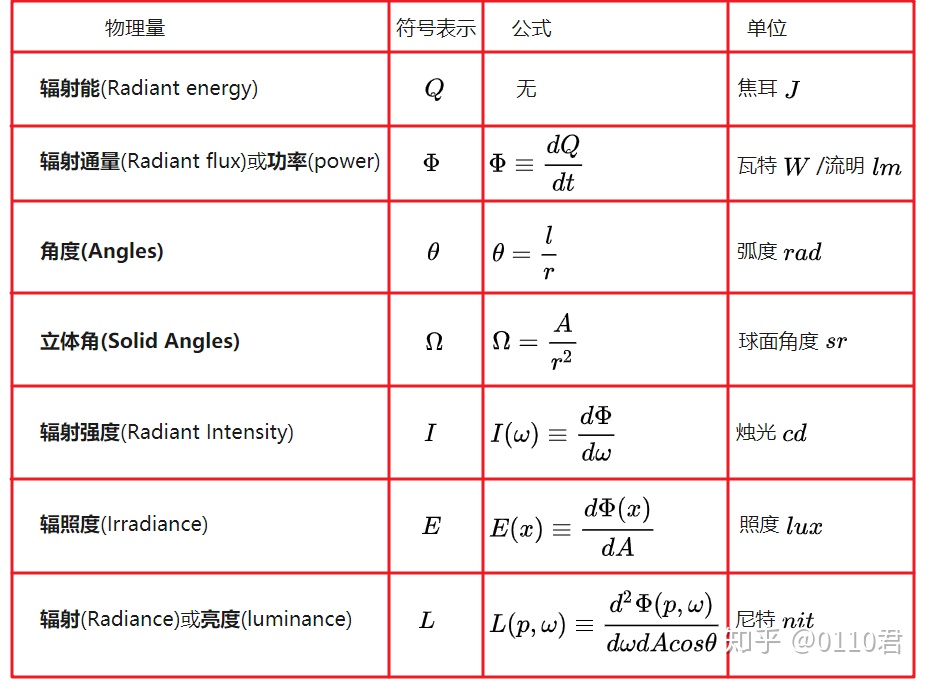
详情可参考：辐射度量学 - 知乎

10.2 some commonly encountered bidirectional reflectance quantities

the bidirectional reflectance $r(i,e,g)$

$$r(i,e,g)= K\frac{\varpi}{4\pi}\frac{\mu_0}{\mu_0+\mu}\left[P(g)+H(\mu_0/K)H(\mu/K)-1\right]$$

the bidirectional reflectance is the ratio of the radiance scattered from the surface of a medium into a given direction to the collimated power incident per area perpendicular to the direction of the incidence.

K is the porosity coefficients.

孔隙率：土壤中孔隙体积与总体积的比值。

$r(i,e,g)=\dfrac{emit_radiance}{incident_irradiance}=\dfrac{I_e}{J}.$

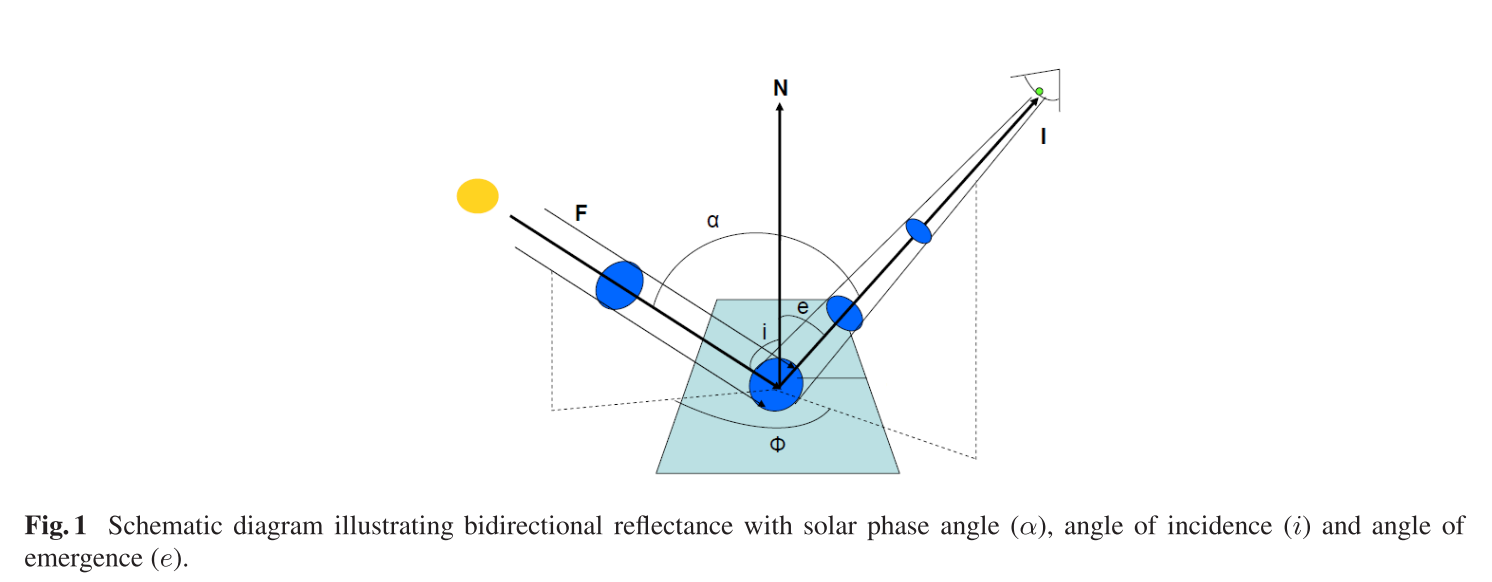
X.-J. Huang et al.: Analysis Based on the Hapke Model and LS Model

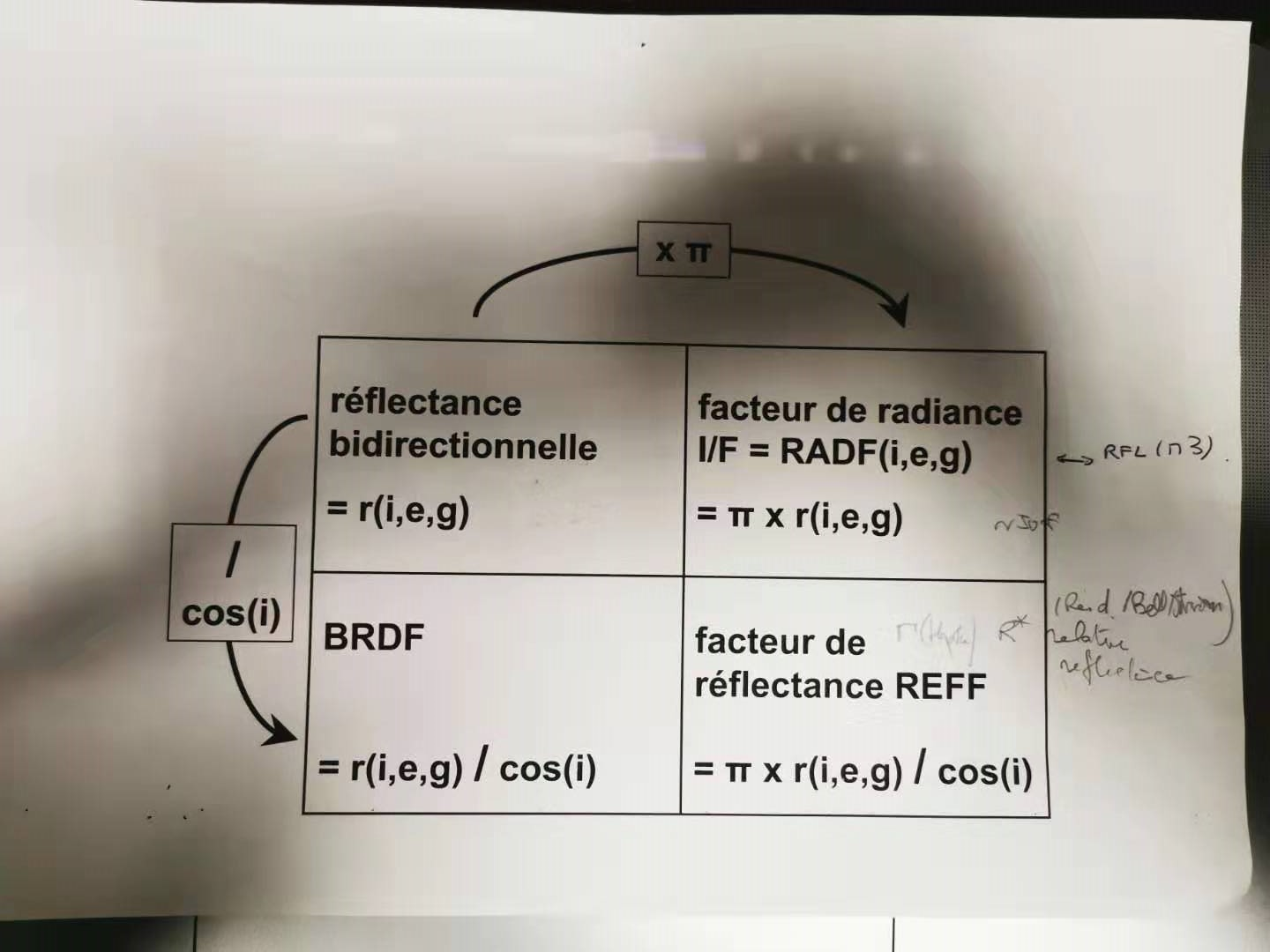
the bidirectional-reflectance distribution function (BDRF)

$$\begin{aligned} BDRF(i,e,g)=&\frac{I}{J\mu_0}=\frac{r(i,e,g)}{\mu_0}\\ =&K\frac{\varpi}{4\pi}\frac{1}{\mu_0+\mu}\left[P(g)+H(\mu_0/K)H(\mu/K)-1\right] \end{aligned}$$

the bidirectional-reflectance distribution function (BDRF) is the ratio of the radiance scattered from the surface of a medium into a given direction to the collimated power incident on a unit area of the surface.

the reflectance factor (REFF), is also called the _reflectance coefficient (or, apparent reflectance)._

$$\small REFF(i,e,g)= \pi r(i,e,g)/\mu_0=K\frac{\varpi}{4}\frac{1}{\mu_0+\mu}\left[P(g)+H(\mu_0/K)H(\mu/K)-1\right]$$

the reflectance factor is the ratio of the reflectance of the surface to that of a perfectly diffuse surface under the same conditions of illumination and measurement.
the bidirectional reflectance of a perfect Lambert surface is

$r_L =\mu_0/\pi$

for details(8.5.1 Lambert’s law)

reflectance factor: 即测量到的反射率$I/J$与相同光照条件下的朗伯体的反射率$\cos i/\pi$之比。

the radiance factor (RADF), is also denoted by I/F.

$$\begin{aligned} RADF(i,e,g)=&\frac{I}{F}(i,e,g)=\pi r(i,e,g) \\=&K\frac{\varpi}{4}\frac{\mu_0}{\mu_0+\mu}\left[P(g)+H(\mu_0/K)H(\mu/K)-1\right] \end{aligned}$$

the radiance factor is the ratio of the bidirectional reflectance of a surface to that of a perfectly diffuse surface illuminated at

$$i = 0,r_L=1/\pi$$

, rather than at the same angle of illumination as the sample.

$F=J/\pi$, Chandrasekhar (1960).

Shkuratov,2011称：在老文章里，也称apparent albedo.（不够准确，权当历史原因造成）。

the relative reflectance ,

$$\begin{aligned} \Gamma(i,e,g)=&\frac{r(Sample)}{r(standard\_surface)}\\ = &\frac{K_{Sa}}{K_{St}}\varpi\frac{P(g)+H(\mu_0/K_{Sa},\varpi)H(\mu/K_{Sa},\varpi)-1}{H(\mu_0/K_{St},\varpi=1)H(\mu/K_{St},\varpi=1)} \end{aligned}$$

the relative reflectance of a particulate sample is the reflectance relative to that of standard surface consisting of an infinitely thick particulate medium of nonabsorbing, isotropic scatterers, with negligible opposition effect, and illuminated and viewed at the same geometry as the sample.

if

$$K_{Sa}=K_{St}\approx 1$$

, and the H functions

$$H(x)\simeq \frac{1+2x}{1+2\gamma x}$$

, the relative bidirectional reflectance of a sample of isotropic scatterers measured outside of the opposition peak is given by

$$\Gamma(i,e,g\gg h)=\frac{\varpi}{(1+2\gamma\mu_0)(1+2\gamma\mu)}$$

the reduced reflectance $r_r(i,e,g)$

$$r_r(i,e,g) =\frac{I/F}{\mu_0/(\mu_0 +\mu)}$$

the reduced reflectance is defined as the radiance factor divided by the Lommel-Seeliger factor.

计算过程中通常还需要校正太阳距离：

• 加州理工大学，喷气动力实验室，JPL：https://ssd.jpl.nasa.gov/horizons.cgi （地平线系统！）

补充知识

反射率波谱

• 方向-方向反射率波谱（晴天，野外便携式地物光谱仪）
• 半球 -方向反射率波谱（阴天）
• 方向-半球反射率波谱（积分球，波谱测定器）;directional-hemispherical reflectance.
• 半球- 半球反射率波谱（等效于反照率光谱）

朗伯体：
朗伯体：是指当入射能量在所有方向均匀反射，即入射能量以入射点为中心，在整个半球空间内向四周各向同性的反射能量的现象，称为漫反射，也称各向同性反射，一个完全的漫射体称为朗伯体。理想的漫反射应遵循这个规律。例如积雪和白墙。
余弦发光体：若一扩展光源的发光强度为dI∝cosθ，即其亮度B与方向无关。这类发射体称为余弦发光体，或朗伯（J.H.Lambert）发光体，上述按cosθ规律发射光通量的规律，成为朗伯余弦定律。式中dI为扩展光表面的每块面元dS沿某方向r的发光强度，θ为r与法线n的夹角。
从远处看，发光球体像是一个发光圆盘，这就是余弦发光体，太阳就是余弦发光体。
物体表面对电磁波的反射有三种形式：

1. 镜面反射：反射能量集中在一个方向，反射角=入射角。
2. 漫反射：整个表面都均匀地向各向反射入射光。
3. 方向反射：介于漫反射和镜面反射之间，各向都有反射，但各向反射强度不均一。实际上多数自然表面对辐射的波长而言都是粗糙表面。当目标物的表面足够粗糙，以致于它对太阳短波辐射的反射辐射亮度在以目标物的中心的2π空间中呈常数，即反射辐射亮度不随观测角度而变，我们称该物体为漫反射体，亦称朗伯体。漫反射又称朗伯(Lambert)反射，也称各向同性反射。

对反射率的一些思考（从量纲量级角度）：

1. 牢记双向反射率的定义：

$$r= I/J \quad [Sr^{-1}]$$

1. 假如没有吸收，且反射在$2\pi$空间内各向同性(朗伯体)，则某一表面

• 入射能量：$P_{in} = J\mu_0 = J (i =0)$
• 出射能量：$P_{out} = \int I cos e d\Omega = \int J r \cos e \sin ede d\varphi = J \pi[Sr] r [Sr^{-1}]$
• 能量守恒：

$$P_{in} = P_{out} \Rightarrow r = {1\over \pi}$$

各种反射率的范围：

BDR = r: 理想朗伯体为$1/\pi$；$[0,1/\pi]$
BDRF = r/cos(i): 范围待分析，本人研究过程中不常用！
RADF = $\pi r$: $[0,1]$
REFF = ${r\over cos i /\pi}$: $[0,1]$ (理想朗伯体的双向反射率最大！)

对理想朗伯体而言，半球反射率与反射率因子在数值上相等：

理想朗伯体的双向反射率：$r = cos i /\pi$

设朗伯体表面积为S,入射辐照度为J,入射角为i,出射角为$\theta$,方位角为$\varphi$,则:
按定义，$r = I/J$
入射通量为：$\Phi_i = J S cos i$
出射通量为：

$\Phi_o = \int I S_\perp d\Omega = \int (rJ)(S cos\theta)d\Omega = rJS \int_0^{2\pi}\int_0^{\pi/2} cos\theta sin\theta d\theta d\varphi = rJS\pi$

按定义，半球反射率，$r_{dh} = {\Phi_o \over \Phi_i}= {rJS\pi \over JS cos i}= {\pi r \over cos i}$
于是，可推导出，$r = r_{dh} cos i/\pi$
进而，按定义，$REFF = {r \over cos i/\pi}= r_{dh}$

1. 考虑入射角为0的朗伯平面（perfectly diffuse surface）：

$$r = 1/\pi$$

• 从反照率

$$A_L= {P_{out} \over J\mu_0} =1 \Rightarrow P_{out} = J = P_{in}; (\mu_0 =1)$$

满足能量守恒

• 从双向反射率：

$$r = I/J = 1/\pi \Rightarrow I = Jr = J/\pi \Rightarrow \\P_{out} = \int_{上半球} I\mu d\Omega = J/\pi \int_{e=0}^{\pi/2} \cos e \sin e de \int_{\psi =0}^{2\pi} = J = P_{in}$$

满足能量守恒

• 但

$$\int_{上半球} r d\Omega = 2 \neq 1$$

• $RADF = \pi r =1$ ;因为完全反射，所以在各个方向上，$RADF=1$。
• 基尔霍夫定律：发射率= 吸收率=1-反射率（在各个方向上都满足），
  • For an arbitrary body emitting and absorbing thermal radiation in thermodynamic equilibrium, the emissivity is equal to the absorptivity.
  • a good absorber is a good emitter, and a poor absorber is a poor emitter,a good reflector must be a poor absorber.
  • In a blackbody enclosure that contains electromagnetic radiation with a certain amount of energy at thermodynamic equilibrium, this “photon gas” will have a Planck distribution of energies.
  • black body radiation is equal in every direction (isotropic), the emissivity and the absorptivity, if they happen to be dependent on direction, must again be equal for any given direction.
  • 此处的反射率不是双向反射率。
  • Kirchhoff ’s law applies to directional–hemispherical reflectance。(Bandfield,2018)
    -