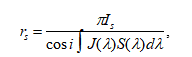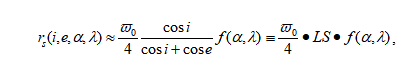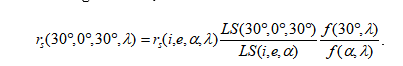Hapke函数

photometric correction： 将反射率校正到相同的光照几何条件下，一般为入射角30°，出射角0°（NASA实验室所采用的）。比值法

$$R_{f-\text {corrected}}=R_{f} \frac{\cos 30^{\circ} /\left(\cos 30^{\circ}+\cos 0^{\circ}\right)}{\cos i^{\prime} /\left(\cos i^{\prime}+\cos e^{\prime}\right)} \frac{f\left(30^{\circ}\right)}{f(g)}$$

• REFF（Reflectance factor）: solar irradiance calibration method
• 
• 

• 经验公式：

注：有两种方法获取绝对反射率

• 定标板
• 太阳辐照度定标方法

• 
• 
• 光度校正的公式（注意式子中的约等号）
• 用Hapke光度模型可以作光度校正，可以反解物性。

---

• 月表光度模型研究进展（许学森，遥感技术与应用）

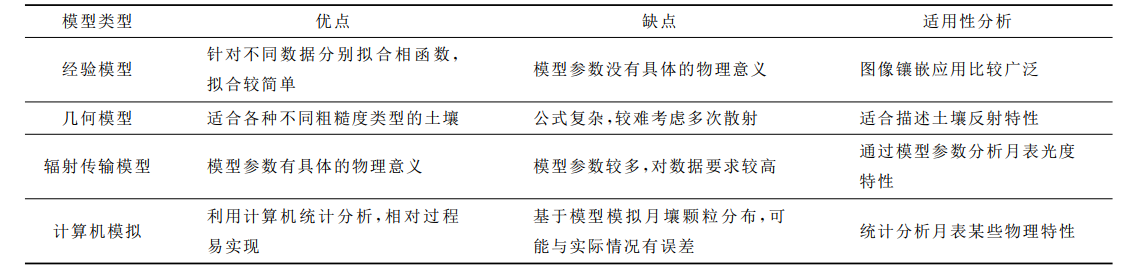
1. 经验模型(hapke8.5节)
2. 几何光学模型
3. 辐射传输模型:Hapke光度模型
4. 计算机数值模拟方法： 蒙托卡罗数值模拟方法

---

Hapke’s photometric model（地大师姐推荐文章(Sato, Robinson et al. 2014)）：也见（Hapke书9.4节（9.47）式）

$$I / F=L S\left(i_{e}, e_{e}\right) K \frac{w}{4}\left[p(g)\left(1+B_{S 0} B_{S}(g)\right)+M\left(i_{e}, e_{e}\right)\right]\left[1+B_{C 0} B_{C}(g)\right] S(i, e, \psi)$$

注：$I/F$为radiance factor，而reflectance factor(REFF)为${I/F\over \pi}$,这里的I/F就是一种表示方法（RADF），不要分开看。

1. LS is the Lommel-Seeliger function,$i_e$ and $e_e$ are effective angle of incidence and emission respectively
2. K is porosity factor,$\phi$,[0,1]
3. w is single scattering albedo,[0,1]
4. p(g) is phase function:b,c；The probability that a photon will be scattered in the direction g is given by p(g)。b,[0,1];c,p(g)>0;
5. $B_{S0}$ is amplitude of Shadow Hiding Opposition Effect (SHOE),Bs,[0,1]
6. $B_S(g)$ is SHOE function,$h_S$
7. $M(i_e, e_e)$ is Isotropic Multiple-Scattering Approximation (IMSA)
8. $B_{C0}$ is amplitude of Coherent Backscatter Opposition Effect (CBOE)，[0,1]
9. $B_C(g)$ is CBOE function,$h_C$
10. S(i,e,𝜓) is shadowing function, and 𝜓 is azimuthal angle between the planes of incidence and emergence；The term $\bar{\theta}_p$ is the shadowing function and corrects for macroscopic roughness of the surface and depends on mean slope angle 𝜃.

1. Henyey-Greenstein double-lobed single particle phase function

$$p(g)=\frac{1+c}{2} \frac{1-b^{2}}{\left(1-2 b \cos (g)+b^{2}\right)^{3 / 2}}+\frac{1-c}{2} \frac{1-b^{2}}{\left(1+2 b \cos (g)+b^{2}\right)^{3 / 2}}$$

b (0 ≤ b ≤ 1) is the shape-controlling parameter, and c (−1 ≤ c ≤ 1) is the relative strength of backward and forward lobes.
b is the angular width of the backward (first term) or forward (second term) scattering lobe and c is the magnitude of the lobe.
c>0,后向；c<0 前向

b控制形状：b越大，侧向散射越弱（b=1例外）

$p(g)=1$ 表示各向同性；$p(g)\neq 1$ 表示各项异性；$p(g) =0$ 表示完全吸收。

• ‘hockey-stick” diagram

$$c=3.29 \exp \left(-17.4 b^{2}\right)-0.908$$

Narrow lobes have b values close to 1, wide lobes have values << 1, and isotropically scattering particles have b = 0; 0 <= b < 1.

Hapke2012,p121

1. The SHOE function BS(g) is given by

$$B_{S}(g)=1 /\left[1+\tan (g / 2) / h_{S}\right]$$

$h_S$ is the angular width parameter of SHOE,

1. The IMSA function $M(i_e, e_e)$ is given by

$$M\left(i_{e}, e_{e}\right)=H\left(\frac{\cos \left(i_{e}\right)}{K}, w\right) H\left(\frac{\cos \left(e_{e}\right)}{K}, w\right)-1$$

where H(x,w) is Ambartsumian-Chandrasekhar H function, which is approximated by

$$H(x, w) \simeq\left\{1-w x\left[r_{0}+\frac{1-2 r_{0} x}{2} \ln \left(\frac{1+x}{x}\right)\right]\right\}^{-1}$$

简化版：

$$H(x)={1+2x\over 1+2\gamma x}$$

$r_0$ is diffusive reflectance, given by

$$r_{0}=\frac{1-\sqrt{1-w}}{1+\sqrt{1-w}}$$

1. The CBOE function $B_C(g)$ is given by

$$B_{C}(g)=\frac{1+\frac{1-\exp \left[-\tan (g / 2) / h_{C}\right]}{\tan (g / 2) / h_{C}}}{2\left[1+\tan (g / 2) / h_{C}\right]^{2}}$$

where $h_C$ is angular width of CBOE

• $h_C = \lambda/4\pi\Lambda$;$\Lambda$ is the transport mean free path in the medium.

1. The porosity factor K is

$$K=\frac{-\ln \left(1-1.209 \phi^{2 / 3}\right)}{1.209 \phi^{2 / 3}}$$

where 𝜙 is filling factor that is equivalent to 1− porosity. The K monotonically increases with the filling factor 𝜙 (= 1− porosity)

孔隙度因子K不同于孔隙度（porosity）

1. The $i_e, e_e,$(注：下标e表示effective) and the shadowing function S(i, e,𝜓) are the functions of $\bar{\theta}_p$ (the mean slope angle), the effective value of the photometric roughness.宏观粗糙度。

公式很复杂，待补充

拟合数据得到如上九个参数，这些参数中有些与物性有关

简化的5参数Hapke模型(地大师姐)：SHOE-only.

$$I / F={\cos i \over \cos i+\cos e}\frac{w}{4}\left[p(g)\left(1+{B_{S 0} \over 1+\tan(g/2)/h_S}\right)+H(\cos i)H(\cos e)-1\right]$$

参数范围：0≤b≤1，-1≤c≤1，0≤w≤1，$0\leq B_{S0} \leq 2$，$0\leq h_S \leq 1$

或者，CBOE-only

在不同的应用场景下，SHOE与CBOE对opposition effects 的贡献不一样，因此，按需选择。得到5参数的hapke模型

$$\begin{aligned} \begin{array}{l} \text {IOF} / L S=\frac{w}{4}\left[p(g)+H\left(\mu_{0}, w\right) H(\mu, w)-1\right]\left[1+B_{C 0} B_{C}\left(g, h_{c}\right)\right] S(i, e, \theta) \\ L S=\mu_{0} /\left(\mu_{0}+\mu\right) \end{array} \end{aligned}$$

简化hapke模型（林洪磊）:仅3个参数，w,b,c

不考虑冲效应，但考虑多次散射，因此得到3参数的hapke模型，

K= 1，因为月壤最上层的填充率未知

忽略SHOE和COBE，因为冲效应仅仅发生在小相角处，而第十月昼的相角大于50°

$$r={\cos i \over \cos i+\cos e}\frac{w}{4\pi}\left[p(g)+H(\cos i)H(\cos e)-1\right]$$

若继续不考虑多次散射，则，hapke模型简化为LS模型

Hapke,2012:

• Single scattering:the Lommel-Seeliger law（p197)

$r = {\varpi \over 4\pi}{\mu_0 \over \mu_0 +\mu}f(g)$

• the bidirectional reflectance of a sparse medium of isotropic scatters(p197)

二流近似

$r = {\varpi \over 4 \pi}{\mu_0\over \mu_0 +\mu}{1+2\mu_0 \over 1+2\gamma\mu_0}{1+2\mu \over 1+2\gamma\mu}$

变分法

$r = {\varpi \over 4 \pi}{\mu_0\over \mu_0 +\mu}H(\mu_0)H(\mu)$

• the isotropic multiple-scattering approximation(IMSA)

$I_{SS} = J{\varpi \over 4\pi}{\mu_0 \over \mu_0 +\mu}p(g)$

$I_{MS} = J{\varpi \over 4 \pi}{\mu_0\over \mu_0 +\mu}[H(\mu_0)H(\mu)-1]$

$r = {\varpi \over 4 \pi}{\mu_0\over \mu_0 +\mu}[p(g)+H(\mu_0)H(\mu)-1]$

for a semi-infinite medium, the multiply scattered portion is much less sensitive to the particle phase function than the singly scattered fraction.

The brighter the surface, the more times the average photon is scattered before emerging from the surface, causing directional effects to be averaged out and the multiply scattered intensity distribution to closely approach the isotropic case.

Since the single-scattering term can be evaluated exactly for an arbitrary phase function and the multiply scattered term is relatively insensitive to phase function, a first-order expression for nonisotropic scatterers can be obtained by using the exact expression for the single-scattered term but retaining the isotropic solution for the multiply-scattered term.

多次散射项不像单次散射项那样对相函数明显，通常，表面越亮，多次散射的次数越多，其方向性就被平均掉了，所以一般多次散射项都当做各向同性处理。

---

一些光度校正的实操论文

问题：参数拟合的数学实现以及遇见的一些细节问题

1. python拟合函数curve_fit

• 参数初始值问题：若不给初值，也不给边界，则初值默认为1；若不给初值，但给定边界，则初值为边界中点。

1. python 其他函数

---

lunar opposition effect（Hapke第九章）

• shadow hiding（占主要）：shadow-hiding mechanism in which particles hide their own shadows at opposition but the shadows quickly become visible as one moves away from opposition（clementine Hillier 1999）
• 相干反向散射coherent backscatter（2°左右的窄峰）： photons following identical but reversed paths can interfere constructively in the backscattering direction, leading to up to a factor of two increase in brightness.
• 具有波长依赖性
• the angular width of the coherent backscatter peak should be proportional to wavelength, it is inversely proportional to the mean optical path length of a photon (which will be smaller in lower albedo surfaces)
• 相干反向散射对更亮的高地地形更重要

ground truth: Apollo site

photometric model 可反演月壤的物理性质

• compaction state
• particle albedo
• particle size
• size distribution
• surface macroscopic roughness
• grain transparency
• porosity
• 光度模型可以反演上述参数，然后用反演的参数与Apollo的“真值”对比，可以检验光度模型理论
• 相对定标：矿物学研究
• 绝对定标： 光度研究、

从反射率光谱获取矿物成分：

• 查找表（lunar spectral mineral lookup table，LUT）
• MGM(修正高斯模型)
• 其他？
  实操过程：

---

光度校正公式（前经验）：

Scattering Law Analysis Based on Hapke and Lommel-Seeliger Models for Asteroidal Taxonomy
Hapke-5parameters

$$\begin{aligned} RADF(i, e, \alpha)&=\frac{\omega}{4} \frac{\mu_{0}}{\mu_{0}+\mu} \\\\ & \times\left\{[1+B(\alpha)] p(\alpha)+H\left(\mu_{0}\right) H(\mu)-1\right\} \\\\ & \times S(i, e, \alpha, \bar{\theta}) \\\\ B(\alpha)&=\frac{B_{\mathrm{so}}}{1+\frac{1}{h_{\mathrm{s}}} \tan \frac{\alpha}{2}} \\\\ p(\alpha)&=\frac{1-g^{2}}{\left(1+2 g \cos \alpha+g^{2}\right)^{\frac{3}{2}}} \\\\ H(x)&=\frac{1+2 x}{1+2 \sqrt{1-\omega} x} \end{aligned}$$

-LS模型

$$\begin{aligned} r(i, e, \alpha)&=A_{\mathrm{ls}} \frac{\mu_{0}}{\mu_{0}+\mu} f(\alpha)\\\\ A_{ls} &={\omega \over 4\pi}\\\\ f(\alpha)&=e^{\beta \alpha+\gamma \alpha^{2}+\delta \alpha^{3}}\\\\ RADF(i,e,\alpha)&= \pi r(i,e,g) \end{aligned}$$

---

光度校正的关键在于获取相函数及其参数。

获取相函数的两种模型：

• Hapke模型
• LS模型

相函数有多种形式：

• HG函数；

$$p(g)=\frac{1+c}{2} \frac{1-b^{2}}{\left(1-2 b \cos (g)+b^{2}\right)^{3 / 2}}+\frac{1-c}{2} \frac{1-b^{2}}{\left(1+2 b \cos (g)+b^{2}\right)^{3 / 2}}$$

b = −0.17, c = 0.70。

• 单参数HG函数

$$p(g)=\frac{1-b^{2}}{\left(1+2 b \cos (g)+b^{2}\right)^{3 / 2}}$$

• $(1/4\pi)\int_{4\pi}p(g)d\Omega = 1$
• $\theta = \pi - g$
• 参数b为余弦不对称因子：$b = <\cos \theta>=-<\cos g>$
• b=0时，$p(g)=1$,各向同性
• b>0时，

• 双参数HG函数

$$p(g)=\frac{1+c}{2} \frac{1-b^{2}}{\left(1-2 b \cos (g)+b^{2}\right)^{3 / 2}}+\frac{1-c}{2} \frac{1-b^{2}}{\left(1+2 b \cos (g)+b^{2}\right)^{3 / 2}}$$

• 第一项为后向项，第二项为前向项；

• 三参数HG函数：$b_1,b_2,c$

• 普通多项式（三阶）

$$f(g)=p_{1} g^{3}+p_{2} g^{2}+p_{3} g+p_{4}$$

• 普通多项式（四阶）

$$f(\alpha)=a_{0}+a_{1} \alpha+a_{2} \alpha^{2}+a_{3} \alpha^{3}+a_{4} \alpha^{4}$$

• 普通多项式（六阶）

$$f(\alpha, \lambda)=\mathrm{A}_{0}+\mathrm{A}_{1} \alpha+\mathrm{A}_{2} \mathrm{a}^{2}+\mathrm{A}_{3} \mathrm{\alpha}^{3}+\mathrm{A}_{4} \mathrm{\alpha}^{4}+\mathrm{A}_{5} \mathrm{\alpha}^{5}+\mathrm{A}_{6} \mathrm{\alpha}^{6}$$

• 普通多项式+指数项（指数项模拟背散射效应）

$$f(\alpha)=b_{0} e^{-b_{1} \alpha}+a_{0}+a_{1} \alpha+a_{2} \alpha^{2}+a_{3} \alpha^{3}+a_{4} \alpha^{4}$$

• 勒让德多项式

$$P(g)=1+b \times \cos (g)+c \times\left(1.5 \times \cos ^{2}(g)-0.5\right)$$

$P_1 = \cos \theta; P_2 = {1\over 2}(3\cos^2\theta -1)$

• 指数形式

$$f(\alpha)=e^{\beta \alpha+\gamma \alpha^{2}+\delta \alpha^{3}}$$

• 其他形式：

三阶多项式
一阶勒让德多项式
线性双项HG函数？

基于得到的相函数做光度校正：

• 比值法
• 解单次反照率：因为多次散射项中包含单次反照率，因此不能直接作比。

以上所有相函数都可用比值法，但HG函数和勒让德多项式来源于Hapke模型，因此还可以基于hapke模型作光度校正

---

光度校正历史

• Clementine （Hiller et al,1999）

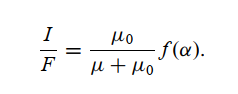
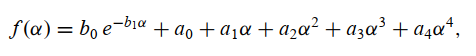
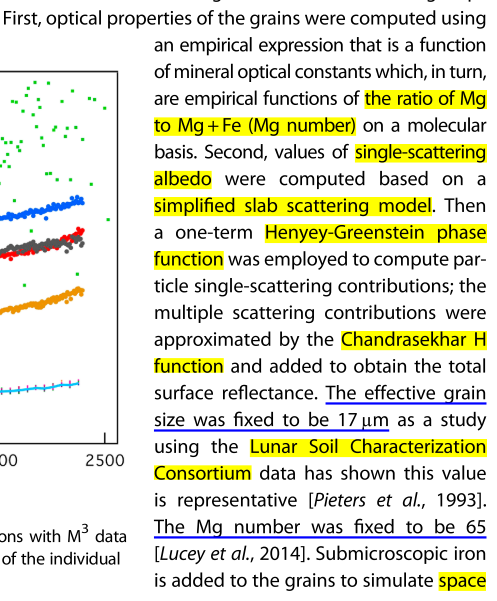
• M3
• SELENE
• CE-1
• CE-3
• CE-4

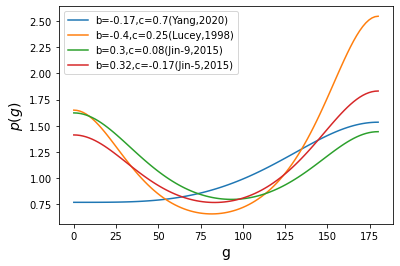
几组HG函数参数：

• b = −0.17， c = 0.70。

(Yang,Yazhou,2020;Lin,Honglei,2020)
CE-4,第十月昼

• b = −0.4, c = 0.25。

(lucey,1998)
假定参数

• b=0.3,c =0.08

(Jin,Weidong,2015)
CE-3,全景相机，460nm,9参数Hapke模型
若使用5参数Hapke模型，b=0.32,c=-0.17

待办

• [ ] 光度模型溯源文章
• [ ] 光端校正文章内容
• [ ] hapke模型

hapke模型的拟合

• 前人怎么拟合的

  网格搜索；遗传算法；查找表，等！

• 求解全局最小的算法及其原理！